题目内容
已知a, b都是正数,并且a ¹ b,求证:a5 + b5 > a2b3 + a3b2
见解析
证明:(a5 + b5 ) - (a2b3 + a3b2) =" (" a5- a3b2) + (b5- a2b3 )
= a3 (a2- b2 ) - b3 (a2- b2) = (a2- b2 ) (a3- b3)
=" (a" + b)(a - b)2(a2 + ab + b2)
∵a, b都是正数,∴a + b, a2 + ab + b2 > 0
又∵a ¹ b,∴(a - b)2 > 0 ∴(a + b)(a - b)2(a2 + ab + b2) > 0
即:a5 + b5 > a2b3 + a3b2
= a3 (a2- b2 ) - b3 (a2- b2) = (a2- b2 ) (a3- b3)
=" (a" + b)(a - b)2(a2 + ab + b2)
∵a, b都是正数,∴a + b, a2 + ab + b2 > 0
又∵a ¹ b,∴(a - b)2 > 0 ∴(a + b)(a - b)2(a2 + ab + b2) > 0
即:a5 + b5 > a2b3 + a3b2

练习册系列答案
相关题目
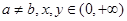 ,求证:
,求证: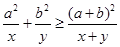 ,指出等号成立的条件;(2)利用(1)的结论求函数
,指出等号成立的条件;(2)利用(1)的结论求函数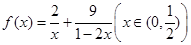 的最小值,指出取最小值时x的值.
的最小值,指出取最小值时x的值.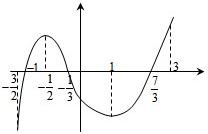
 ≥a恒成立,则实数a的最大值为_____________.
≥a恒成立,则实数a的最大值为_____________.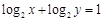 ,则x + y的最小值为 .
,则x + y的最小值为 .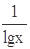 ≥2
≥2 +
+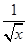 ≥2
≥2 的最小值为2
的最小值为2
 +
+ ≥2
≥2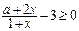 的解集
的解集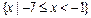 ,则实数
,则实数 =___________.
=___________.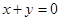 ,则
,则 的最小值是( )
的最小值是( )