题目内容
已知函数f(x)=x|x-a|,(a∈R),若a=2,解关于x的不等式f(x)<x.
当a=2时,不等式f(x)<x即x|x-2|<x,
显然x≠0,
当x>0时,原不等式可化为:|x-2|<1⇒-1<x-2<1⇒1<x<3;
当x<0时,原不等式可化为:|x-2|>1⇒x-2>1或x-2<-1⇒x>3或x<1
∴x<0;
综上得:当a=2时,原不等式的解集为{x|1<x<3或x<0}.
显然x≠0,
当x>0时,原不等式可化为:|x-2|<1⇒-1<x-2<1⇒1<x<3;
当x<0时,原不等式可化为:|x-2|>1⇒x-2>1或x-2<-1⇒x>3或x<1
∴x<0;
综上得:当a=2时,原不等式的解集为{x|1<x<3或x<0}.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
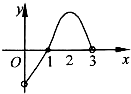
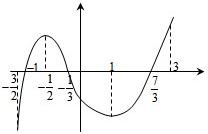
 ≥a恒成立,则实数a的最大值为_____________.
≥a恒成立,则实数a的最大值为_____________.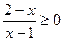 的解集是 。
的解集是 。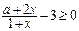 的解集
的解集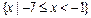 ,则实数
,则实数 =___________.
=___________.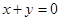 ,则
,则 的最小值是( )
的最小值是( )