题目内容
【题目】已知函数![]() 是
是![]() 上的偶函数,对于任意
上的偶函数,对于任意![]() 都有
都有![]() 成立,当
成立,当![]() ,且
,且![]() 时,都有
时,都有![]() .给出以下三个命题:
.给出以下三个命题:
①直线![]() 是函数
是函数![]() 图像的一条对称轴;
图像的一条对称轴;
②函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
③函数![]() 在区间
在区间![]() 上有五个零点.
上有五个零点.
问:以上命题中正确的个数有( ).
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
根据题意,利用特殊值法分析可得![]() ,结合函数的奇偶性可得
,结合函数的奇偶性可得![]() ,
,
进而可得![]() ,所以
,所以![]() 的周期为6;据此分析三个命题,综合即可得答案.
的周期为6;据此分析三个命题,综合即可得答案.
解:根据题意,对于任意![]() ,都有
,都有![]() 成立,
成立,
令![]() ,则
,则![]() ,
,
又![]() 是
是![]() 上的偶函数,所以
上的偶函数,所以![]() ,则有
,则有![]() ,所以
,所以![]() 的周期为6;
的周期为6;
据此分析三个命题:
对于①,函数为偶函数,则函数的一条对称轴为![]() 轴,又由函数的周期为6,
轴,又由函数的周期为6,
则直线![]() 是函数
是函数![]() 图象的一条对称轴,①正确;
图象的一条对称轴,①正确;
对于②,当![]() ,
,![]() ,
,![]() ,且
,且![]() 时,都有
时,都有![]() ,
,
则函数![]() 在
在![]() ,
,![]() 上为增函数,
上为增函数,
因为![]() 是
是![]() 上的偶函数,所以函数
上的偶函数,所以函数![]() 在
在![]() ,
,![]() 上为减函数,
上为减函数,
而![]() 的周期为6,所以函数
的周期为6,所以函数![]() 在
在![]() ,
,![]() 上为减函数,②错误;
上为减函数,②错误;
对于③,![]() (3)
(3)![]() ,
,![]() 的周期为6,
的周期为6,
所以![]() ,
,
函数![]() 在
在![]() ,
,![]() 上有四个零点;③错误;
上有四个零点;③错误;
三个命题中只有①是正确的;
故选:B.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 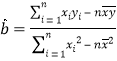 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
【题目】某校计划面向高二年级文科学生开设社会科学类和自然退坡在校本选修课程,某文科班有50名学生,对该班选课情况进行统计可知:女生占班级人数的60%,选社会科学类的人数占班级人数的70%,男生有10人选自然科学类.
(1)根据题意完成以下![]() 列联表:
列联表:
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 |
(2)判断是否有99%的把握认为科类的选择与性别有关?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: ,其中
,其中![]() .
.