题目内容
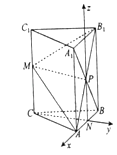
【题目】如图,在三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AC=BC=5,AB=6,M是CC1中点,CC1=8. 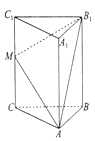
(1)求证:平面AB1M⊥平面A1ABB1;
(2)求平面AB1M与平面ABC所成二面角的正弦值.
【答案】
(1)证明:连结A1B,交AB1于点P,
∵三棱柱ABC﹣A1B1C1中,四边形ABB1A1是矩形,∴P是A1B的中点,
取AB的中点N,连结CN,PN,MP,
则NP∥CM,且NP=CM,∴四边形MCNP是平行四边形,
∴CN∥MP,
又AC=BC,∴CN⊥AB,
∵CC1⊥平面ABC,∴CC1⊥CN,
又AA1∥CC1,∴CN⊥AA1,
∴CN⊥平面A1ABB1,∴MP⊥平面A1ABB1,
∵MP平面AB1M,∴平面AB1M⊥平面A1ABB1.
(2)解:以N为原点,NA为x轴,CN为y轴,NP为z轴,建立空间直角坐标系,
∵AC=BC=5,AB=6,M是CC1中点,CC1=8,
∴A(3,0,0),M(0,﹣4,4),B1(﹣3,0,8),
![]() =(﹣3,﹣4,4),
=(﹣3,﹣4,4), ![]() =(﹣6,0,8),
=(﹣6,0,8),
设平面AB1M的法向量 ![]() =(x,y,z),
=(x,y,z),
则 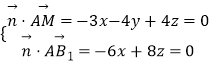 ,取x=4,得
,取x=4,得 ![]() =(4,0,3),
=(4,0,3),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
设平面AB1M与平面ABC所成二面角的平面角为θ,
则cosθ= 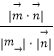 =
= ![]() ,sinθ=
,sinθ= ![]() =
= ![]() .
.
∴平面AB1M与平面ABC所成二面角的正弦值为 ![]() .
.
【解析】(1)连结A1B,交AB1于点P,取AB的中点N,连结CN,PN,MP,推导出四边形MCNP是平行四边形,从而CN∥MP,进而CC1⊥CN,由AA1∥CC1 , 知CN⊥AA1 , 从而CN⊥平面A1ABB1 , 进而MP⊥平面A1ABB1 , 由此能证明平面AB1M⊥平面A1ABB1 . (2)以N为原点,NA为x轴,CN为y轴,NP为z轴,建立空间直角坐标系,利用向量法能求出平面AB1M与平面ABC所成二面角的正弦值.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案