题目内容
【题目】已知h(x)=|2x﹣1|+m|x+3|(m>0),且h(x)的最小值是7. (Ⅰ)求m的值;
(Ⅱ)求出当h(x)取得最小值时x的取值范围.
【答案】解:(Ⅰ)h(x)=|2x﹣1|+m|x+3|=|1﹣2x|+|mx+3m|≥|(m﹣2)x+(1+3m)|, ∵h(x)的最小值是7,故 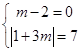 ,解得:m=2;
,解得:m=2;
(Ⅱ)由(Ⅰ)得,当且仅当(1﹣2x)(mx+3m)≥0(2x﹣1)(2x+6)≤0,
即﹣3≤x≤ ![]() 时,h(x)≥|(m﹣2)x+(1+3m)|中的“=”成立,
时,h(x)≥|(m﹣2)x+(1+3m)|中的“=”成立,
故h(x)取最小值时x的范围是[﹣3, ![]() ].
].
【解析】(Ⅰ)根据不等式的性质得到关于m的方程组,解出即可;(Ⅱ)根据“=”成立的条件求出x的范围即可.
【考点精析】通过灵活运用绝对值不等式的解法,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号即可以解答此题.

练习册系列答案
相关题目