题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,向量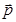 =(sinA,b+c),
=(sinA,b+c),
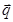 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足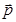 ⊥
⊥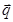 ,则角B=( )
,则角B=( )
A.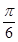 B.
B.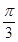 C.
C.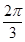 D.
D.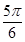
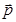 =(sinA,b+c),
=(sinA,b+c),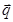 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足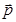 ⊥
⊥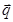 ,则角B=( )
,则角B=( )A.
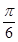 B.
B.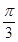 C.
C.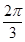 D.
D.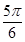
B
试题分析:因为
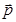 ⊥
⊥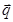 所以
所以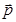 ·
·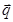 =(sinA,b+c)·(a-c,sinC-sinB)=0,
=(sinA,b+c)·(a-c,sinC-sinB)=0,即(a-c)sinA+(b+c)(sinC-sinB)=0,
由正弦定理得(a-c)a +(b+c)(c- b)=0,即
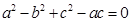 ,
,所以cosB=
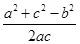 =
=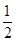 ,又
,又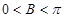 ,所以角B=
,所以角B=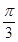 ,选B。
,选B。点评:综合题,两向量垂直,则它们的数量积为0.

练习册系列答案
相关题目
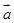 |=1,|
|=1,|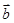 | =
| =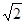 且(
且(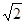 时,存在某个位置,使得AB⊥CD
时,存在某个位置,使得AB⊥CD x>0时,都不存在某个位置,使得AB⊥CD
x>0时,都不存在某个位置,使得AB⊥CD :
: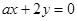 的方向向量是
的方向向量是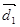 ,直线
,直线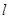 2 :
2 :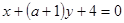 的法向量是
的法向量是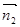 ,若
,若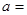 _________.
_________. 分)已知
分)已知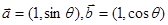 ,
,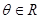 ;
;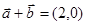 ,求
,求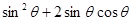 的值;
的值;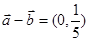 ,
,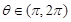 ,求
,求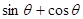 的值.
的值.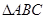 中,设
中,设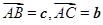 ,点
,点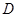 在
在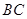 边上且
边上且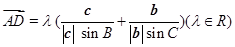 ,则
,则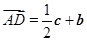
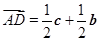
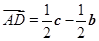
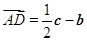
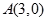 ,
, ,
,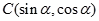 ,其中
,其中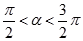 ,
,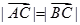 ,求
,求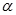 的值
的值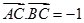 ,求
,求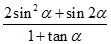 的值
的值 是单位正方体
是单位正方体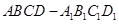 中异于点
中异于点 的一个顶点,则
的一个顶点,则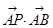 的值为( )
的值为( ) 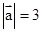 ,
,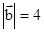 ,且(
,且(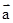 +k
+k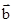 )⊥(
)⊥( k
k