题目内容
3.函数f(x)=|x2-2x+$\frac{1}{2}$|-$\frac{3}{2}$x+1的零点个数为2.分析 构造函数设g(x)=|x2-2x+$\frac{1}{2}$|,k(x)=$\frac{3}{2}$x-1,画出图象,运用图象的交点得出有关函数的零点个数.
解答 解:设g(x)=|x2-2x+$\frac{1}{2}$|,k(x)=$\frac{3}{2}$x-1,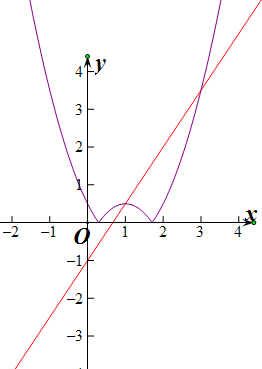
根据图象得出g(x)与k(x)有2个交点,
∴f(x)=|x2-2x+$\frac{1}{2}$|-$\frac{3}{2}$x+1的零点个数为2
故答案为:2;
点评 本题考查了函数交点问题与函数的零点的问题的关系,数学结合的思想的运用,属于中档题,关键是构造函数,画出图象.

练习册系列答案
相关题目
14.要得到函数y=cosx的图象,只需将函数$y=sin(2x+\frac{π}{3})$的图象上所有的点的( )
| A. | 横坐标伸长到原来的2倍(纵坐标不变),再向左平移$\frac{π}{6}$个单位长度 | |
| B. | 横坐标伸长到原来的2倍(纵坐标不变),再向右平移$\frac{π}{3}$个单位长度 | |
| C. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向左平移$\frac{π}{6}$个单位长度 | |
| D. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向右平移$\frac{π}{3}$个单位长度 |