题目内容
(14分)某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动)。该校合唱团共有100名学生,他们参加活动的次数统计如图所示。
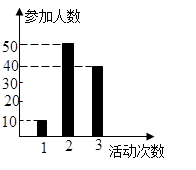
⑴求合唱团学生参加活动的人均次数;
⑵从合唱团中任选两名学生,求他们参加活动次数恰好相等的概率;
⑶从合唱团中任选两名学生,用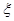 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量
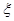 的分布列及数学期望
的分布列及数学期望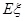 。
。
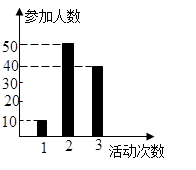
⑴求合唱团学生参加活动的人均次数;
⑵从合唱团中任选两名学生,求他们参加活动次数恰好相等的概率;
⑶从合唱团中任选两名学生,用
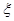 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量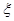 的分布列及数学期望
的分布列及数学期望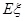 。
。⑴参加活动的人均次数为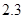
⑵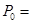
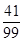
⑶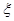 的分布列
的分布列
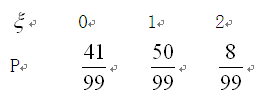
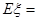
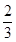
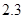
⑵
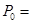
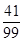
⑶
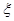 的分布列
的分布列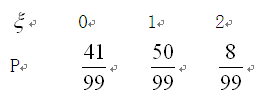
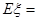
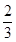
本试题主要是考查了条形图的运用,以及古典概型概率的运算,和分布列的求解和数学期望值的综合运用。
(1)由图可知,参加活动1次、2次和3次的学生人数分别10、50和40.
⑴该合唱团学生参加活动的人均次数为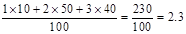
(2)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为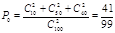
(3)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件A,“这两人中一人参加2次活动,另一人参加3次”为事件B,“这两人中一人参加1次活动,另一人参加3次活动”为事件C,那么容易知道各个取值的概率值,进而得到分布列。
解:由图可知,参加活动1次、2次和3次的学生人数分别10、50和40.
⑴该合唱团学生参加活动的人均次数为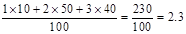 ……………(2分)
……………(2分)
⑵从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为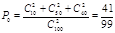 ………(4分)
………(4分)
⑶从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件A,“这两人中一人参加2次活动,另一人参加3次”为事件B,“这两人中一人参加1次活动,另一人参加3次活动”为事件C。 易知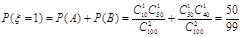 ………(6分)
………(6分)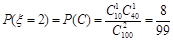 …………(8分)
…………(8分) 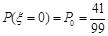 ……………(10分)
……………(10分)
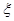 的分布列
的分布列
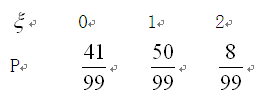

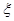 的数学期望:
的数学期望: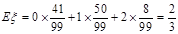 ………………………(14分)
………………………(14分)
(1)由图可知,参加活动1次、2次和3次的学生人数分别10、50和40.
⑴该合唱团学生参加活动的人均次数为
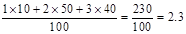
(2)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为
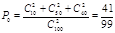
(3)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件A,“这两人中一人参加2次活动,另一人参加3次”为事件B,“这两人中一人参加1次活动,另一人参加3次活动”为事件C,那么容易知道各个取值的概率值,进而得到分布列。
解:由图可知,参加活动1次、2次和3次的学生人数分别10、50和40.
⑴该合唱团学生参加活动的人均次数为
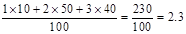 ……………(2分)
……………(2分)⑵从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为
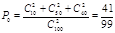 ………(4分)
………(4分)⑶从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件A,“这两人中一人参加2次活动,另一人参加3次”为事件B,“这两人中一人参加1次活动,另一人参加3次活动”为事件C。 易知
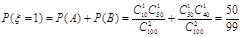 ………(6分)
………(6分)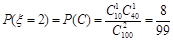 …………(8分)
…………(8分) 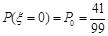 ……………(10分)
……………(10分)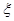 的分布列
的分布列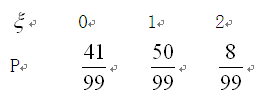

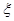 的数学期望:
的数学期望: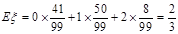 ………………………(14分)
………………………(14分)
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


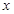 ,
,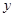 的值;
的值;
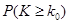

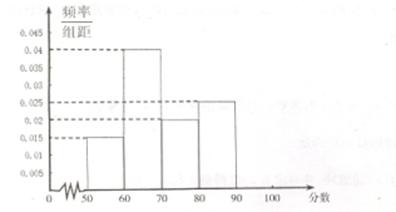
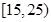
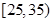
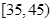
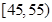
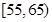
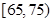
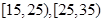 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“楼市限购令”人数为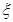 ,求随机变量
,求随机变量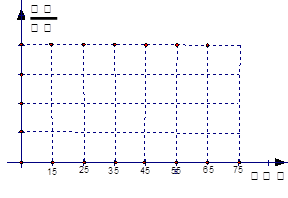
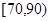 段的有多少人?
段的有多少人?

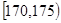
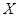 为这两名学生来自第3组的人数,求
为这两名学生来自第3组的人数,求