题目内容
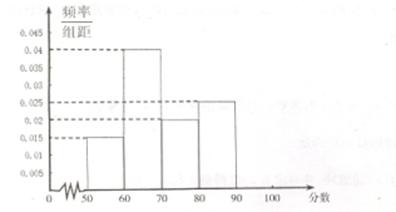
为抗击金融风暴,某系统决定对所属企业给予低息贷款的扶持,该系统制定了评分标准,并根据标准对企业进行评估,然后依据评估得分将这些企业分别定为优秀、良好、合格、不合格四个等级,并根据等级分配相应的低息贷款数额,为了更好地掌握贷款总额,该系统随机抽查了所属的部分企业.一下图表给出了有关数据(将频率看做概率)
(1)任抽一家所属企业,求抽到的企业等级是优秀或良好的概率;
(2)对照标准,企业进行了整改.整改后,如果优秀企业数量不变,不合格企业、合格企业、良好企业的数量成等差数列.要使所属企业获得贷款的平均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数百分比的最大值是多少?
(1)任抽一家所属企业,求抽到的企业等级是优秀或良好的概率;
(2)对照标准,企业进行了整改.整改后,如果优秀企业数量不变,不合格企业、合格企业、良好企业的数量成等差数列.要使所属企业获得贷款的平均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数百分比的最大值是多少?


(1)0.45.(2)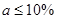
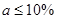
(Ⅰ)设任意抽取一家企业,抽到良好企业、优秀企业的概率分别是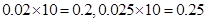 ,所以抽到的企业是优秀或良好企业的概率为0.2+0.25=0.45.
,所以抽到的企业是优秀或良好企业的概率为0.2+0.25=0.45.
(Ⅱ)整改后优秀企业的频率为0.25,由不合格企业,合格企业,良好企业的频率成等差数列.设该等差数列的首项为a,公差为d,则3a+3d=1-0.25=0.75,即a+d=0.25,设整改后一家企业获得的低息贷款为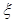 ,然后列出分布列,求出
,然后列出分布列,求出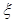 的数学期望,再由
的数学期望,再由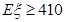 可得到关于a的不等式从而求出a的取值范围.
可得到关于a的不等式从而求出a的取值范围.
解:(1)设任意抽取一家企业,抽到不合格企业、合格企业、良好企业、优秀企业的概率分别是p1、p2、p3、p4
则根据频率分布直方图可知:

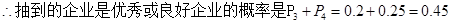
(2) 设整改后,任意抽取一家企业,抽到不合格企业、合格企业、良好企业的概率分别为
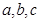 ,
,
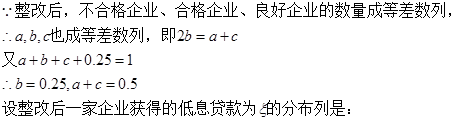

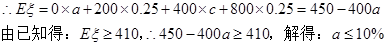 …………13分
…………13分
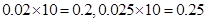 ,所以抽到的企业是优秀或良好企业的概率为0.2+0.25=0.45.
,所以抽到的企业是优秀或良好企业的概率为0.2+0.25=0.45.(Ⅱ)整改后优秀企业的频率为0.25,由不合格企业,合格企业,良好企业的频率成等差数列.设该等差数列的首项为a,公差为d,则3a+3d=1-0.25=0.75,即a+d=0.25,设整改后一家企业获得的低息贷款为
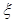 ,然后列出分布列,求出
,然后列出分布列,求出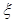 的数学期望,再由
的数学期望,再由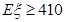 可得到关于a的不等式从而求出a的取值范围.
可得到关于a的不等式从而求出a的取值范围.解:(1)设任意抽取一家企业,抽到不合格企业、合格企业、良好企业、优秀企业的概率分别是p1、p2、p3、p4
则根据频率分布直方图可知:

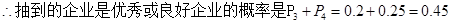
(2) 设整改后,任意抽取一家企业,抽到不合格企业、合格企业、良好企业的概率分别为
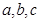 ,
,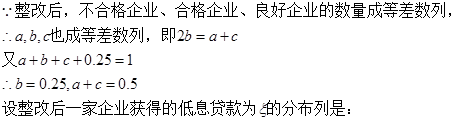

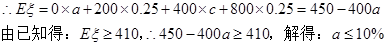 …………13分
…………13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,
, 值,并补全频数条形图;
值,并补全频数条形图;





 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)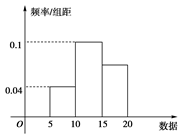


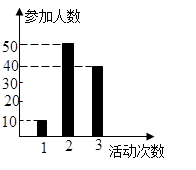
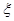 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量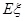 。
。