题目内容
已知数列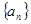 满足
满足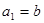 ,
,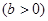 ,
,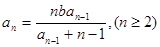 .
.
(1)求数列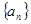 的通项公式;
的通项公式;
(2)证明:对于一切正整数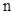 ,有
,有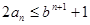 .
.
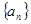 满足
满足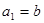 ,
,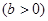 ,
,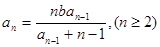 .
.(1)求数列
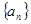 的通项公式;
的通项公式;(2)证明:对于一切正整数
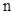 ,有
,有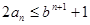 .
.(1) 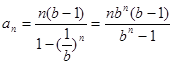 (2)见解析
(2)见解析
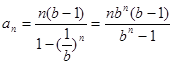 (2)见解析
(2)见解析(1)由题意可知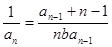 ,进而可得
,进而可得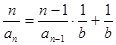 ,
,
令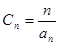 ,
,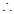
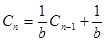 ,然后讨论b=1和
,然后讨论b=1和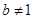 ,
,
当b=1时,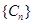 是等差数列.其通项公式易求.
是等差数列.其通项公式易求.
当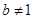 时,要构造等比数列
时,要构造等比数列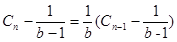 ,
,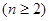 ,说明数列
,说明数列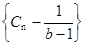 为等比数列,易求其通项公式,进而求出Cn.
为等比数列,易求其通项公式,进而求出Cn.
(2) (ⅰ)当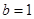 时,
时,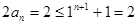 成立;
成立;
当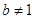 时,
时, ,
,
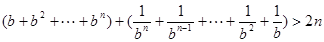 ,
,
然后根据等比数列前n项和公式进行研究即可.
解:(1)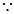
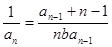 ,
,
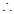
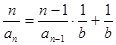 令
令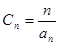
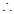
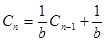 ------------2分
------------2分
(ⅰ)当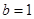 时,
时,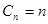
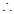
 ------- 4分
------- 4分
(ⅱ)当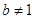 时,
时,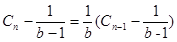 ,
,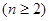
数列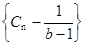 为等比数列,所以,
为等比数列,所以,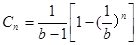
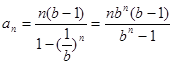 --------- 8分
--------- 8分
(2)证明: (ⅰ)当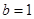 时,
时,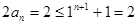 --------------10分
--------------10分
(ⅱ)当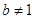 时,
时,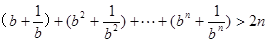
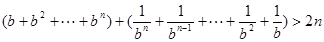
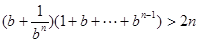
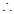
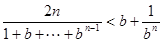

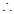
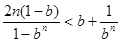
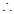
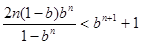
即;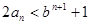
所以:对于一切正整数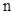 ,有
,有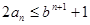 .----------------15分
.----------------15分
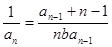 ,进而可得
,进而可得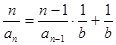 ,
,令
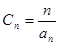 ,
,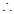
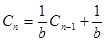 ,然后讨论b=1和
,然后讨论b=1和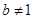 ,
,当b=1时,
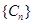 是等差数列.其通项公式易求.
是等差数列.其通项公式易求.当
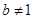 时,要构造等比数列
时,要构造等比数列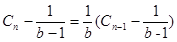 ,
,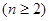 ,说明数列
,说明数列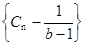 为等比数列,易求其通项公式,进而求出Cn.
为等比数列,易求其通项公式,进而求出Cn.(2) (ⅰ)当
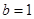 时,
时,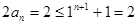 成立;
成立;当
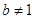 时,
时, ,
,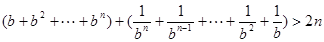 ,
,然后根据等比数列前n项和公式进行研究即可.
解:(1)
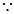
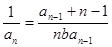 ,
,
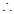
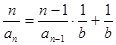 令
令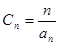
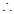
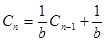 ------------2分
------------2分(ⅰ)当
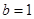 时,
时,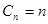
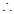
 ------- 4分
------- 4分(ⅱ)当
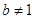 时,
时,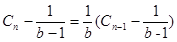 ,
,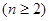
数列
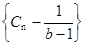 为等比数列,所以,
为等比数列,所以,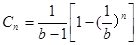
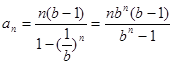 --------- 8分
--------- 8分(2)证明: (ⅰ)当
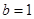 时,
时,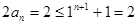 --------------10分
--------------10分(ⅱ)当
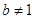 时,
时,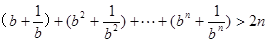
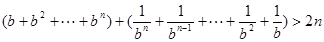
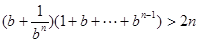
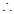
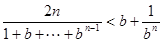

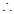
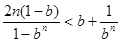
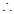
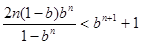
即;
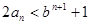
所以:对于一切正整数
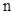 ,有
,有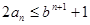 .----------------15分
.----------------15分
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的前
的前 项和为
项和为 ,
, ,则
,则





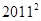 .
.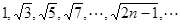 ,则
,则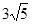 是该数列的第( )项。
是该数列的第( )项。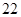

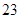

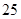
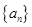 满足
满足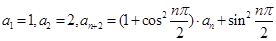 ,则该数列的前10项的和为
,则该数列的前10项的和为 
 则当
则当 时,n的最小值是
时,n的最小值是 对任意的
对任意的 有
有 ,若
,若 ,则
,则 .
.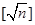 表示不超过
表示不超过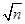 的最大整数。
的最大整数。
 。
。