题目内容
20.一个平面和一个球相切于A点,从球面上一点B作该平面的垂线BC,垂足是C.若AC=2$\sqrt{3}$,BC=2,则此球的表面积等于64π.分析 如图,设从点B作平面a的垂线与球面的另一个交点为B′,求出BB′,进而求出球的半径,即可求出球的表面积.
解答  解:如图,设从点B作平面a的垂线与球面的另一个交点为B′,由圆幂定理CB×CB′=CA2,得CB′=6cm,BB′=CB′-CB=4cm,
解:如图,设从点B作平面a的垂线与球面的另一个交点为B′,由圆幂定理CB×CB′=CA2,得CB′=6cm,BB′=CB′-CB=4cm,
设弦BB′的中点为E,连接OE(O为球心),有OE⊥BB′,那么OE∥AC,又OA?a,BC?a,得OA∥BC,所以球的半径为r=OA=CE=4(cm).
∴球的表面积等于4π•42=64π.
故答案为:64π.
点评 本题考查求球的表面积,考查学生的计算能力,求出球的半径是关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
10.某班同学利用暑假在A、B两个小区逐户进行了一次生活习惯是否符合低碳观念的调查及宣传活动.若生活习惯符合低碳观念的称为“低碳族”,否则,称为“非低碳族”.各小区中,这两“族”人数分别与本小区总人数的比值如下表:
(Ⅰ)如果甲、乙来自A小区,丙、丁来自B小区,求这4人中恰有2人是“低碳族”的概率;
(Ⅱ)经过大力宣传后的连续两周,A小区“非低碳族”中,每周有20%的人加入到“低碳族”的行列.这两周后,如果从A小区中随机地选出25个人,用ξ表示这25个人中的“低碳族”人数,求数学期望E(ξ).
| 低碳族 | 非低碳族 | |
| 比值(A小区) | $\frac{1}{2}$ | $\frac{1}{2}$ |
| 比值(B小区) | $\frac{4}{5}$ | $\frac{1}{5}$ |
(Ⅱ)经过大力宣传后的连续两周,A小区“非低碳族”中,每周有20%的人加入到“低碳族”的行列.这两周后,如果从A小区中随机地选出25个人,用ξ表示这25个人中的“低碳族”人数,求数学期望E(ξ).
5.已知集合$A=\{x|y=\sqrt{{{log}_2}x}\},B=\{y|y=\frac{1}{2^x},x>0\}$,则A∩CRB=( )
| A. | (0,1) | B. | (-∞,1] | C. | [1,+∞) | D. | φ |
12.已知圆(x-a)2+(y-b)2=1与两直线l1:3x-4y-1=0和l2:4x+3y+1=0都有公共点,则$\frac{b}{a+2}$的取值范围为( )
| A. | [-$\frac{1}{2}$,$\frac{1}{4}$] | B. | [$\frac{1}{4}$,$\frac{3}{4}$] | C. | (-∞,-$\frac{1}{2}$]∪[$\frac{3}{4}$,+∞) | D. | [-$\frac{21}{22}$,$\frac{14}{27}$] |
9.要得到函数y=sin(x+$\frac{π}{6}$)的图象,只需要将函数y=cosx的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
10.三个数0.42,20.4,log0.42的大小关系为( )
| A. | 0.42<20.4<log0.42 | B. | log0.42<0.42<20.4 | ||
| C. | 0.42<log0.42<20.4 | D. | log0.42<20.4<0.42 |
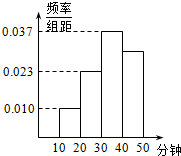 某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在40~50分钟的人数为81.
某健康协会从某地区睡前看手机的居民中随机选取了270人进行调查,得到如右图所示的频率分布直方图,则可以估计睡前看手机在40~50分钟的人数为81.