题目内容
已知实数集R,集合M={x||x-2|≤2},集合N={x|y=
},则M∩(CRN)=( )
| 1 | ||
|
分析:先将M、N化简,求出CRN,再求M∩(CRN)即可.
解答:解:由|x-2|≤2得0≤x≤4,所以M={x|0≤x≤4},
由x-1>0,得x>1,所以N={x|x>1},CRN={x|x≤1},
∴M∩(CRN)={x|0≤x≤1}
故选B
由x-1>0,得x>1,所以N={x|x>1},CRN={x|x≤1},
∴M∩(CRN)={x|0≤x≤1}
故选B
点评:本题考查了集合的含义、表示方法,集合的交、并、补集的混合运算,属于基础题.本题中N表示的是函数的定义域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数集R,集合M={x||x+2|<2},N={x|
<1},则M∩(?R N)=( )
| 3 |
| x+1 |
| A、{x|-4<x<0} |
| B、{x|-1<x≤0} |
| C、{x|-1≤x<0} |
| D、{x|x<0,或x>2} |
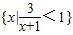 ,则M∩(∁R N)=( )
,则M∩(∁R N)=( )