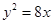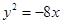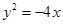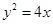题目内容
已知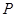 是双曲线
是双曲线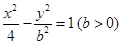 上一点,
上一点, 、
、 是其左、右焦点,
是其左、右焦点,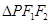 的三边长成等差数列,且
的三边长成等差数列,且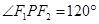 ,则双曲线的离心率等于
,则双曲线的离心率等于
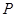 是双曲线
是双曲线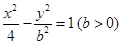 上一点,
上一点,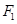 、
、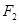 是其左、右焦点,
是其左、右焦点,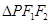 的三边长成等差数列,且
的三边长成等差数列,且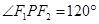 ,则双曲线的离心率等于
,则双曲线的离心率等于A. | B.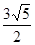 | C.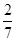 | D.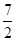 |
D
试题分析:由题意,可根据双曲线的定义及题设中三边长度成等差数列得出方程|PF1|-|PF2|=4与2|PF1|=|PF2|+2c,由此两方程可解出|PF1|=2c-4,|PF2|=2c-8,再由∠F1 P F2=120°,由余弦定理建立关于c的方程,解出c的值,即可由公式求出离心率的值. 解:由题,不妨令点P在右支上,如图,则有,|PF1|-|PF2|=4 ①,2|PF1|=|PF2|+2c ②,由①②解得|PF1|=2c-4,|PF2|=2c-8,又∠F1 P F2=120°,由余弦定理得,4c2=(2c-4)2+(2c-8)2+(2c-4)×(2c-8),解得,c=7或c=2(舍),又a=2,故e=
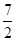 故答案为 D
故答案为 D点评:本题考查双曲线的简单性质及等差数列的性质,解题的关键是熟练掌握基础知识且能灵活选用基础知识建立方程求参数,本题考查了方程的思想及转化的思想

练习册系列答案
相关题目
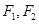 分别为双曲线
分别为双曲线 (a>0,b>0)的左、右焦点,
(a>0,b>0)的左、右焦点, 为双曲线左支上的任意一点,若
为双曲线左支上的任意一点,若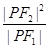 的最小值为
的最小值为 ,则双曲线离心率
,则双曲线离心率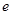 的取值范围是( )
的取值范围是( )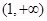
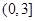
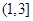

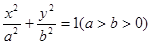 上一点,且
上一点,且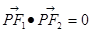 ,
,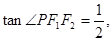 则该椭圆的离心率为( )
则该椭圆的离心率为( )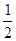
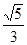
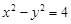 ,直线
,直线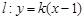 与该双曲线只有一个公共点,
与该双曲线只有一个公共点, :
: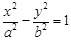
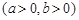 的离心率
的离心率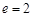 ,过双曲线
,过双曲线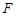 作
作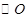 :
: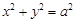 的两条切线,切点分别为
的两条切线,切点分别为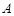 、
、 ,则
,则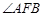 的大小等于( )
的大小等于( ) 是抛物线
是抛物线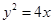 的焦点,准线与
的焦点,准线与 轴的交点为
轴的交点为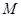 ,点
,点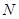 在抛物线上,且
在抛物线上,且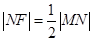 ,则
,则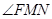 等于( )
等于( )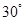
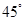

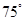
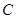 的顶点为坐标原点
的顶点为坐标原点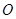 ,焦点
,焦点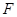 在
在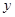 轴上,准线
轴上,准线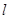 与圆
与圆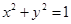 相切.
相切.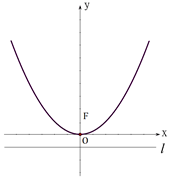
 和抛物线
和抛物线 ,命题P:“若直线
,命题P:“若直线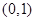 ,则
,则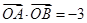 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。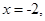 则抛物线的方程是( )
则抛物线的方程是( )