题目内容
18.关于x的不等式|x-1|-|x|-|m+1|>0的解集非空,则实数m的取值范围是(2,0).分析 由题意可得|x-1|-|x|>|m+1|的解集非空,根据绝对值的意义求得|x-1|-|x|的最大值为1,可得1>|m+1|,由此求得实数m的取值范围.
解答 解:由题意可得|x-1|-|x|>|m+1|的解集非空.
由于|x-1|-|x|表示数轴上的x对应点到1对应点的距离减去它到0对应点的距离,
故|x-1|-|x|的最大值为1,故有1>|m+1|,即-1<m+1<1,解得-2<m<0,
故答案为:(-2,0).
点评 本题主要考查绝对值的意义,绝对值不等式的解法,函数的能成立问题,属于中档题.

练习册系列答案
相关题目
9.已知全集U=R,A={x|x<1},B={y|-|x|+y=2},则集合∁U(A∪B)=( )
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
3.若复数$\frac{a+i}{2i}$的实部和虚部相等,则实数a等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
10.若复数Z满足$\overline Z$(1+i)=2i,则在复平面内Z对应的点的坐标是( )
| A. | (1,1) | B. | (1,-l) | C. | (-l,1) | D. | (-l,-l) |
8.函数f(x)=sin(x+$\frac{π}{2}$)图象的一个对称中心为( )
| A. | ($\frac{π}{2}$,0) | B. | (0,1) | C. | (0,0) | D. | (-$\frac{π}{4}$,0) |
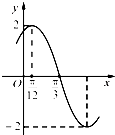 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )