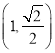题目内容
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,离心率
,离心率![]() ,且椭圆经过点
,且椭圆经过点![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 是菱形,且点
是菱形,且点![]() 在椭圆上.若存在,求出
在椭圆上.若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(![]() )
)![]() .(
.(![]() )
)![]() 或
或![]() .(
.(![]() )存在,点
)存在,点![]() .
.
【解析】试题分析:(1)由题意求出椭圆方程![]() ;(2)联立方程组得到韦达定理,由弦长公式求得
;(2)联立方程组得到韦达定理,由弦长公式求得![]() ,得到直线方程;(3)由特殊位置直线
,得到直线方程;(3)由特殊位置直线![]() 垂直
垂直![]() 轴时,易知存在点
轴时,易知存在点![]() 满足四边形
满足四边形![]() 是菱形。
是菱形。
试题解析:
(![]() )由题意可得
)由题意可得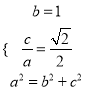 ,解得
,解得![]() ,
, ![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(![]() )设直线
)设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,则
,则
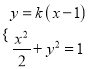 ,消去
,消去![]() 得
得![]() ,
,
![]() ,
, ![]() .
.
∵![]() ,
,
∴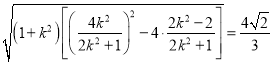 ,
,
化简得![]() 即
即![]() ,
,
解得![]() .
.
故直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)存在点![]() 满足要求。
满足要求。
当直线![]() 垂直
垂直![]() 轴时,则
轴时,则![]() 时,即
时,即![]() ,
, ![]() 在右顶点
在右顶点![]() 时,则四边形
时,则四边形![]() 是菱形,所以存在满足要求的点
是菱形,所以存在满足要求的点![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目