题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,证明:点
,证明:点![]() 总在直线
总在直线![]() 上.
上.
【答案】(1)![]() ;(2)祥见解析.
;(2)祥见解析.
【解析】试题分析:(1)由已知,可求![]() ,
,![]() ,故方程为
,故方程为![]() ;(2)当直线
;(2)当直线![]() 不与
不与![]() 轴垂直时,设直线
轴垂直时,设直线![]() 的方程为
的方程为![]() 、
、![]() ,由
,由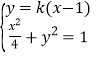 得
得![]() ,由
,由![]() 共线,得
共线,得![]() ,又
,又![]() ,则
,则![]() ,代入可得结论.
,代入可得结论.
试题解析:(1)由题意知:![]() ,
,
∵椭圆上的点![]() 满足
满足![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]()
又∵![]() ,∴
,∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() ,
,
(2)由题意知![]() ,
,
①当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,则
,则![]() 的方程是:
的方程是:![]() ,
,
![]() 的方程是:
的方程是:![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)当直线![]() 不与
不与![]() 轴垂直时,设直线
轴垂直时,设直线![]() 的方程为
的方程为![]() 、
、![]() ,
,
由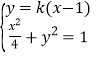 得
得![]() ,
,
∴![]() .
.
![]() ,
,![]() 共线,∴
共线,∴![]() .
.
又![]() ,需证明
,需证明![]() 共线,
共线,
需证明![]() ,只需证明
,只需证明![]() ,
,
若![]() ,显然成立,若
,显然成立,若![]() ,即证明
,即证明![]()
![]() 成立.
成立.
∴![]() 共线,即点
共线,即点![]() 总在直线
总在直线![]() 上.
上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】收入是衡量一个地区经济发展水平的重要标志之一,影响收入的因素有很多,为分析学历对收入的作用,某地区调查机构欲对本地区进行了此项调查.

(1)你认为应采用何种抽样方法进行调查?
(2)经调查得到本科学历月均收入条形图如图,试估算本科学历月均收入![]() 的值?
的值?
(3)设学年为![]() ,令
,令![]() ,月均收入为
,月均收入为![]() ,已知调查机构调查结果如下表
,已知调查机构调查结果如下表
学历 (年) | 小学 | 初中 | 高中 | 本科 | 硕士生 | 博士生 |
| 6 | 9 | 12 | 16 | 19 | 22 |
| 2.0 | 2.7 | 3.7 | 5.8 | 7.8 | |
| 2210 | 2410 | 2910 |
| 6960 |
从散点图中可看出![]() 和
和![]() 的关系可以近似看成是一次函数图像. 若回归直线方程为
的关系可以近似看成是一次函数图像. 若回归直线方程为![]() ,试预测博士生的平均月收入.
,试预测博士生的平均月收入.