题目内容
已知梯形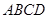 中
中 ,
,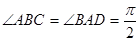 ,
,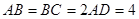 ,
, 、
、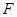 分别是
分别是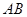 、
、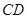 上的点,
上的点,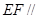
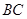 ,
,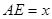 .沿
.沿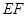 将梯形
将梯形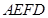 翻折,使平面
翻折,使平面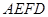 ⊥平面
⊥平面 (如图).
(如图).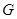 是
是 的中点.
的中点.
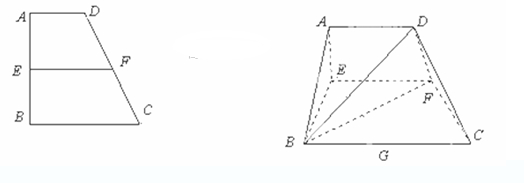
(1)当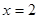 时,求证:
时,求证: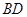 ⊥
⊥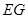 ;
;
(2)当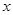 变化时,求三棱锥
变化时,求三棱锥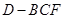 体积的最大值.
体积的最大值.
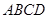 中
中 ,
,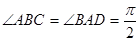 ,
,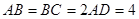 ,
,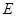 、
、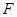 分别是
分别是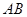 、
、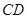 上的点,
上的点,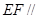
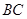 ,
,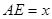 .沿
.沿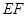 将梯形
将梯形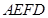 翻折,使平面
翻折,使平面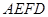 ⊥平面
⊥平面 (如图).
(如图). 是
是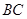 的中点.
的中点.
(1)当
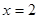 时,求证:
时,求证: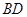 ⊥
⊥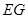 ;
;(2)当
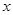 变化时,求三棱锥
变化时,求三棱锥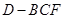 体积的最大值.
体积的最大值. (1)证明过程详见解析;(2)当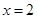 时,最大值为
时,最大值为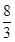 .
.
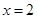 时,最大值为
时,最大值为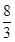 .
.试题分析:本题主要考查空间两条直线的位置关系、直线与平面垂直等基础知识,考查空间想象能力、运算能力和推理论证能力.第一问,先作辅助线
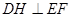 ,由面面垂直的性质得
,由面面垂直的性质得 平面
平面 ,所以
,所以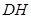 垂直于面内的线
垂直于面内的线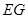 ,又可以由已知证出四边形
,又可以由已知证出四边形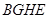 为正方形,所以
为正方形,所以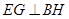 ,再利用线面垂直的判定证明
,再利用线面垂直的判定证明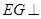 平面
平面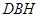 ,从而得
,从而得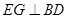 ;第二问,由已知,利用线面垂直的判定证明
;第二问,由已知,利用线面垂直的判定证明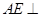 面
面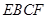 ,结合第一问的结论
,结合第一问的结论 平面
平面 ,得
,得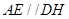 ,设出三棱锥的高,列出体积公式,通过配方法求最大值.
,设出三棱锥的高,列出体积公式,通过配方法求最大值.试题解析:(1)证明:作
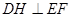 ,交
,交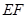 与
与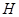 ,连结
,连结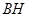 ,
,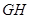 , 1分
, 1分∵平面
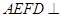 平面
平面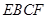 ,交线
,交线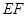 ,
,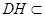 平面
平面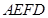 ,
,∴
 平面
平面 ,又
,又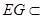 平面
平面 ,故
,故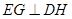 . 3分
. 3分∵
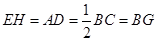 ,
, ,
, .
.∴四边形
 为正方形,故
为正方形,故 . 5分
. 5分又
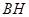 、
、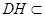 平面
平面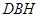 ,且
,且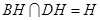 ,故
,故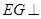 平面
平面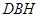 .
.又
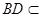 平面
平面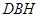 ,故
,故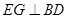 . 6分
. 6分(2)解:∵
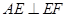 ,平面
,平面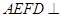 平面
平面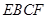 ,交线
,交线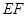 ,
,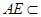 平面
平面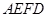 .
.∴
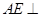 面
面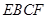 .又由(1)
.又由(1) 平面
平面 ,故
,故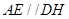 , 7分
, 7分∴四边形
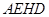 是矩形,
是矩形,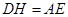 ,故以
,故以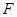 、
、 、
、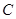 、
、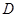 为顶点的三
为顶点的三棱锥
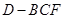 的高
的高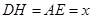 . 9分
. 9分又
 . 10分
. 10分∴三棱锥
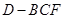 的体积
的体积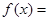
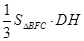
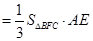
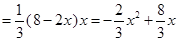 (
(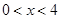 )
)当
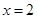 时,最大值为
时,最大值为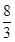 12分
12分
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 的正方形
的正方形 和等腰直角三角形
和等腰直角三角形 按图拼为新的几何图形,
按图拼为新的几何图形, 中,
中, ,连结
,连结 ,若
,若 ,
, 为
为 中点
中点
 与
与 所成角的大小;
所成角的大小; 为
为 中点,证明:
中点,证明: 平面
平面 ;
; 平面
平面
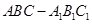 中,
中,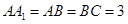 ,
,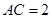 ,
,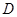 是
是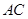 的中点.
的中点.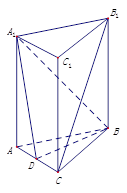
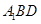 平面
平面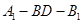 的余弦值.
的余弦值.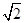 和a且长为a的棱与长为
和a且长为a的棱与长为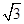 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )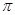
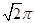
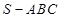 中,
中,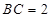 ,
,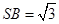 ,
,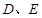 分别是棱
分别是棱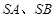 上的点,
上的点,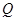 为边
为边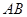 的中点,
的中点, ,则三角形
,则三角形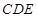 的面积为 .
的面积为 .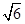 、 3,则这个三棱锥的外接球的表面积为 ( )
、 3,则这个三棱锥的外接球的表面积为 ( ) B.
B. C.
C.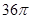 D.
D.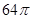
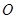 是棱长为
是棱长为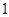 的正方体
的正方体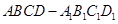 的内切球,则平面
的内切球,则平面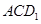 截球
截球
 是平面图形
是平面图形 的直观图,则
的直观图,则