题目内容
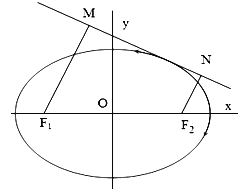
【题目】已知圆![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作圆的切线
作圆的切线![]() 、
、![]() ,切点为
,切点为![]() 、
、![]() .
.
(1)当![]() 的横坐标为
的横坐标为![]() 时,求
时,求![]() 的大小;
的大小;
(2)求四边形![]() 面积的最小值;
面积的最小值;
(3)求证:经过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 必过定点,并求出所有定点的坐标.
必过定点,并求出所有定点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析,
;(3)证明见解析,![]() ,
,![]()
【解析】
(1)由已知求出![]() 点纵坐标,求出
点纵坐标,求出![]() ,利用
,利用![]() ,求出
,求出![]() ,即可得出结论;
,即可得出结论;
(2)![]() ,转化求
,转化求![]() 的最小值,求圆心到直线
的最小值,求圆心到直线![]() 的最小值,即可求解;
的最小值,即可求解;
(3)设![]() ,由
,由![]() ,圆
,圆![]() 就是以
就是以![]() 为直径的圆,求出其方程,整理为圆系方程,即可求解.
为直径的圆,求出其方程,整理为圆系方程,即可求解.
(1)由题可知,圆![]() 的半径
的半径![]() ,
,![]() ,
,
因为![]() 是圆
是圆![]() 的一条切线,所以
的一条切线,所以![]() ,
,
又因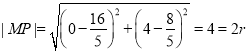 ,
,
又![]() ,
,![]() ;
;
(2)![]() ,
,
要使四边形![]() 面积最小,只需
面积最小,只需![]() 最小.
最小.
又![]() ,只需
,只需![]() 最小.
最小.
当![]() 时,
时,![]() 有最小值,
有最小值,![]() ,
,
![]() 此时四边形面积最小为
此时四边形面积最小为![]() .
.
(3)设![]() ,因为
,因为![]() ,
,
所以经过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 以
以![]() 为直径,
为直径,
方程为: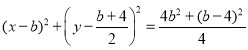
即![]()
由![]() ,解得
,解得![]() 或
或![]()
所以圆过定点![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目