题目内容
【题目】如图，将长为4，宽为1的长方形折叠成长方体ABCD-A1B1C1D1的四个侧面，记底面上一边
，连接A1B,A1C,A1D.
（1）求长方体ABCD-A1B1C1D1体积的最大值 ；
（2）当长方体ABCD-A1B1C1D1的体积最大时，求二面角B-A1C-D的大小.
【答案】(1)1;(2)
【解析】
（1）用
表示出长方体ABCD-A1B1C1D1体积为：
，
，求该二次函数类型函数的最大值即可。
（2）由（1）得
时，长方体ABCD-A1B1C1D1体积最大，此时该几何体为正方体，过点
作
垂直A1C于点E，连接ED，则
就是二面角B-A1C-D的一个平面角，解三角形
即可。
（1）长方体ABCD-A1B1C1D1体积为：，，当时，
，所以长方体ABCD-A1B1C1D1体积的最大值为1.
（2）由（1）得时，长方体ABCD-A1B1C1D1体积最大，此时该几何体为正方体，过点作垂直A1C于点E，连接ED，
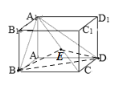
由正方体可得：
,所以就是二面角B-A1C-D的一个平面角，
在正方体ABCD-A1B1C1D1中可得：
，
，
在三角形由余弦定理得：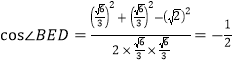
所以
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
