题目内容
在平面直角坐标系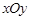 中,圆
中,圆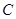 的方程为
的方程为 ,若直线
,若直线 上
上
至少存在一点,使得以该点为圆心,1为半径的圆与圆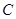 有公共点,则
有公共点,则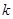 的最大值是 ▲ .
的最大值是 ▲ .
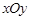 中,圆
中,圆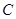 的方程为
的方程为 ,若直线
,若直线 上
上至少存在一点,使得以该点为圆心,1为半径的圆与圆
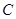 有公共点,则
有公共点,则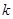 的最大值是 ▲ .
的最大值是 ▲ . 。
。【考点】圆与圆的位置关系,点到直线的距离
∵圆C的方程可化为: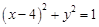 ,∴圆C的圆心为
,∴圆C的圆心为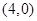 ,半径为1。
,半径为1。
∵由题意,直线 上至少存在一点
上至少存在一点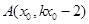 ,以该点为圆心,1为半径的圆与圆
,以该点为圆心,1为半径的圆与圆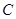 有公共点;
有公共点;
∴存在 ,使得
,使得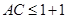 成立,即
成立,即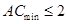 。
。
∵ 即为点
即为点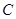 到直线
到直线 的距离
的距离 ,∴
,∴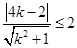 ,解得
,解得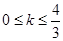 。
。
∴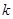 的最大值是
的最大值是
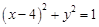 ,∴圆C的圆心为
,∴圆C的圆心为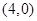 ,半径为1。
,半径为1。∵由题意,直线
 上至少存在一点
上至少存在一点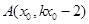 ,以该点为圆心,1为半径的圆与圆
,以该点为圆心,1为半径的圆与圆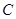 有公共点;
有公共点;∴存在
 ,使得
,使得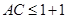 成立,即
成立,即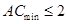 。
。∵
 即为点
即为点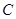 到直线
到直线 的距离
的距离 ,∴
,∴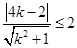 ,解得
,解得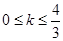 。
。∴
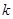 的最大值是
的最大值是

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
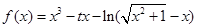 ,对于任意实数
,对于任意实数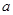 ,
,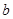
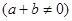 ,都有
,都有 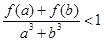 ,则实数
,则实数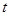 的取值范围是 ( )
的取值范围是 ( )
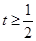


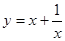 在
在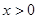 时有 ( )
时有 ( ) .
.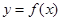 在点
在点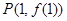 处的切线与直线
处的切线与直线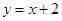 垂直,求函数
垂直,求函数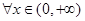 都有
都有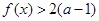 成立,试求
成立,试求 的取值范围;
的取值范围;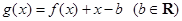 .当
.当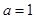 时,函数
时,函数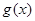 在区间
在区间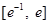 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.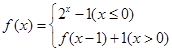 ,则
,则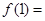 ( )
( )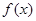 在
在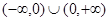 上有意义,且在
上有意义,且在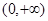 上是增函数,
上是增函数,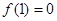
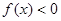 的实数
的实数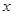 的取值范围;
的取值范围;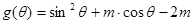 ,若集合
,若集合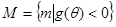 ,集合
,集合 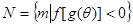 ,求
,求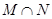
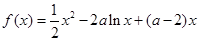 ,
,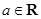 .
.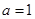 时,求函数
时,求函数 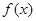 的最小值;
的最小值; 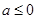 时,讨论函数
时,讨论函数 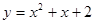 ,
,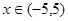 的单调减区间为( )
的单调减区间为( )
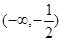
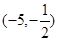
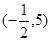
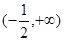
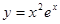 的单调递减区间是. ( )
的单调递减区间是. ( )