题目内容
【题目】如图，已知O为△ABC的外心，角A、B、C的对边分别为a、b、c．
（1）若5 
+4 
+3 
= 
，求cos∠BOC的值；
（2）若 
= 
，求 
的值． 
【答案】
（1）解：∵5 
+4 
+3 
= 
，即4 +3 =﹣5 ，
两边平方，可得：4R2+9R2+24 =25R2
得24 =0
即| || |cos∠BOC=0，
∴cos∠BOC=0．
（2）解：∵ 
= 
，
∴ （ 
）= （ 
），即 
可得：﹣R2cos2A+R2cos2B=﹣R2cos2C+R2cos2A
∴2cos2A=cos2C+cos2B，
即2（1﹣2sin2A）=2﹣（2sin2B+2sin2C），
2sin2A=﹣sin2B+sin2C，
可得2a2=﹣b2+c2，
那么： 
=2．
【解析】
【考点精析】认真审题，首先需要了解余弦定理的定义(余弦定理:
;
;
)．
练习册系列答案
相关题目
【题目】为了解某地区某种农产品的年产量x（单位：吨）对价格y（单位：千元/吨）和利润z的影响，对近五年该农产品的年产量和价格统计如表：
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
（Ⅰ）求y关于x的线性回归方程 
；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润z取到最大值？（保留两位小数）
参考公式： 
= 
= 
， 
．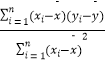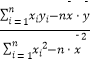