题目内容
已知函数f(x)＝Asin(ωx＋
)＋B(A＞0，ω＞0，||＜
)的一系列对应值如下表：
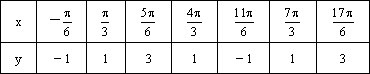
(Ⅰ)根据表格提供的数据求函数f(x)的一个解析式；
(Ⅱ)根据(1)的结果，若函数y＝f(kx)(k＞0)周期为
，当x∈[0，
]时，方程f(kx)＝m恰有两个不同的解，求实数m的取值范围；
答案：
解析：
解析：
|
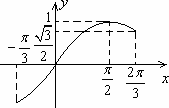
解：(1)设f(x)的最小正周期为T，得 由 又 令 ∴ (2)∵函数 又k＞0 ∴k＝3 6分 令 如图sint＝s在
∴方程f(kx)＝m在 即实数的取值范围是 |
2分
得
，解得
3分
，即
，解得
6分
的周期为
，∵
∴
9分
上有两个不同的解的充要条件是
，
14分
练习册系列答案
相关题目
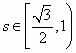
(a、b为常数)，且方程f(x)－x＋12＝0有两个实根为x1＝3，x2＝4.
.
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
)