题目内容
抛物线y=ax2+bx+c与x轴的两个交点为(-
,0),(
,0),则ax2+bx+c>0的解的情况是( )
| 2 |
| 2 |
A.-
| B.x>
| ||||||||
C.x≠±
| D.不确定,与a的符号有关 |
分两种情况考虑:
(i)当a>0时,抛物线开口向上,
∵抛物线y=ax2+bx+c与x轴的两个交点为(-
,0),(
,0),
∴ax2+bx+c>0的解集为:x<-
或x>
;
(ii)当a<0时,抛物线开口向下,
∵抛物线y=ax2+bx+c与x轴的两个交点为(-
,0),(
,0),
∴ax2+bx+c>0的解集为:-
<x<
,
则ax2+bx+c>0的解的情况是不确定,与a的符合有关.
故选D
(i)当a>0时,抛物线开口向上,
∵抛物线y=ax2+bx+c与x轴的两个交点为(-
| 2 |
| 2 |
∴ax2+bx+c>0的解集为:x<-
| 2 |
| 2 |
(ii)当a<0时,抛物线开口向下,
∵抛物线y=ax2+bx+c与x轴的两个交点为(-
| 2 |
| 2 |
∴ax2+bx+c>0的解集为:-
| 2 |
| 2 |
则ax2+bx+c>0的解的情况是不确定,与a的符合有关.
故选D

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
抛物线y=ax2与直线y=kx+b(k≠0)交于A,B两点,且此两点的横坐标分别为x1,x2,直线与x轴的交点的横坐标是x3,则恒有( )
| A、x3=x1+x2 | B、x1x2=x1x3+x2x3 | C、x3+x1+x2=0 | D、x1x2+x1x3+x2x3=0 |
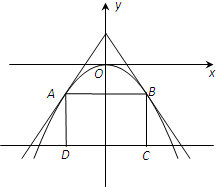 如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.
如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.