题目内容
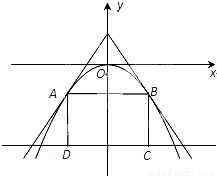
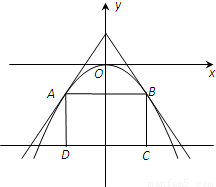
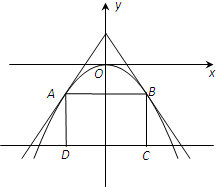 如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.
如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.分析:设切点为(x0,y0),则y0=-ax02,把点(0,a3)代入切线方程求得x0=±a,y0=-a3,可得AB=2a,BC=8-a3,所以矩形面积为S=16a-2a4(0<a<2 ),由S'=16-8a3,可得当a=
时,S有最大值为12
.
| 3 | 2 |
| 3 | 2 |
解答:解:设切点为(x0,y0),则y0=-ax02.
因为y'=-2ax,所以切线方程为y-y0=-2ax0(x-x0),即y+ax02=-2ax0(x-x0),---(2分)
因为切线过点(0,a3),所以a3+ax02=-2ax0(0-x0),即a3=ax02,于是x0=±a.-----(2分)
将代入 y0=-ax02 得,y0=-a3.-----(2分)
(若设切线方程为y=kx+a3,代入抛物线方程后由△=0得到切点坐标,亦予认可.)
所以AB=2a,BC=8-a3,所以矩形面积为S=16a-2a4(0<a<2).----(3分)
于是S'=16-8a3.所以当0<a<
时,S'>0;当
<a<2时,S'<0;
故当a=
时,S有最大值为12
.----(3分)
因为y'=-2ax,所以切线方程为y-y0=-2ax0(x-x0),即y+ax02=-2ax0(x-x0),---(2分)
因为切线过点(0,a3),所以a3+ax02=-2ax0(0-x0),即a3=ax02,于是x0=±a.-----(2分)
将代入 y0=-ax02 得,y0=-a3.-----(2分)
(若设切线方程为y=kx+a3,代入抛物线方程后由△=0得到切点坐标,亦予认可.)
所以AB=2a,BC=8-a3,所以矩形面积为S=16a-2a4(0<a<2).----(3分)
于是S'=16-8a3.所以当0<a<
| 3 | 2 |
| 3 | 2 |
故当a=
| 3 | 2 |
| 3 | 2 |
点评:本题主要考查抛物线的标准方程,以及简单性质的应用,函数在某一点的导数的几何意义,利用导数判断函数的单调性,利用单调性求函数的最值.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.
如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.