题目内容
(本小题满分14分)
己知.函数![]() 的反函数是
的反函数是![]() .设数列
.设数列![]() 的前n项和为
的前n项和为![]() ,对任意的正整数都有
,对任意的正整数都有![]() 成立,且
成立,且![]() •
•
(I)求数列![]() 的通项公式; ,
的通项公式; ,
(II)记![]() ,设数列
,设数列![]() 的前n项和为
的前n项和为![]() ,求证:对任意正整数n都有
,求证:对任意正整数n都有![]() ;
;
(III)设数列![]() 的前n项和为
的前n项和为![]() ,已知正实数
,已知正实数![]() 满足:对任意正整数n,
满足:对任意正整数n,![]() 恒成立,求
恒成立,求![]() 的最小值
的最小值
|
又an+1=5sn+1+1![]()
![]() 数列
数列![]() 成等比数列,其首项
成等比数列,其首项![]() ,公比是
,公比是![]() ………2分
………2分
![]() ,
,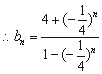 ………..3分高考高考资源
………..3分高考高考资源
(Ⅱ)由(Ⅰ)知![]()
![]()
= ![]() ...............(文)9分、(理)4分
...............(文)9分、(理)4分
又![]() ,当
,当![]() 成立, ………….(文)10分、(理)5分,
成立, ………….(文)10分、(理)5分,
当n≥2时,Tn<![]()
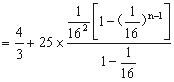 <
<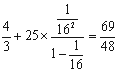 <
<![]()
………………………………………(文)14分、(理)7分
(Ⅲ)由(Ⅰ)知![]() ,一方面,已知
,一方面,已知![]() 恒成立,取n为大于1的奇数时,设
恒成立,取n为大于1的奇数时,设![]() 则Rn=b1+b2+…+b2k+1=4n+5
则Rn=b1+b2+…+b2k+1=4n+5![]()
![]() >
>![]()
![]() 对一切大于1的奇数n恒成立
对一切大于1的奇数n恒成立
![]() 只对满足
只对满足![]() 的正奇数n成立,矛盾 .…..........9分
的正奇数n成立,矛盾 .…..........9分
另一方面,当![]() 时,对一切的正整数n都有
时,对一切的正整数n都有![]() ,事实上,对任意的正整数k,有
,事实上,对任意的正整数k,有
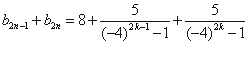
![]()
![]()
![]() 当n为偶数时,设
当n为偶数时,设![]() ,则
,则
![]() <
<![]() …………11分
…………11分
当n为奇数时,设![]() w。w-w*k&s%5¥u
w。w-w*k&s%5¥u
则![]() …
…![]()
![]() 对一切的正整数n,都有
对一切的正整数n,都有![]() ,综上所述,正实数
,综上所述,正实数![]() 的最小值为4 …………..….14分
的最小值为4 …………..….14分

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)