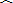题目内容

设圆（x-2）2+（y-2）2=4的切线l与两坐标轴交于点A（a，0），B（0，b），ab≠0．
（1）证明：（a-4）（b-4）=8；
（2）若a＞4，b＞4，求△AOB的面积的最小值．
（1）证明：直线l的方程为
x
a
+
y
b
=1，即bx+ay-ab=0，
则圆心（2，2）到切线l的距离d=r，即
|2b+2a-ab|
b2+a2
=2，
整理得：ab-4（a+b）+8=0，
则（a-4）（b-4）=8；
（2）由（a-4）（b-4）=8，得到ab=4（a+b）-8，
又a＞4，b＞4，
∴S△AOB=
1
2
ab=2[（a-4）+（b-4）+6]≥2（2
(a-4)(b-4)
+6）=4（3+2
2
），（当且仅当a=b=4+2
2
时取等号），
则△AOB面积的最小值是12+8
2
．
练习册系列答案
相关题目
过点Q(-2，
21
)作圆O：x2+y2=r2（r＞0）的切线，切点为D，且QD=4．
（1）求r的值；
（2）设P是圆O上位于第一象限内的任意一点，过点P作圆C的切线l，且l交x轴于点A，交y轴于点B，设
OK
=
OA
+
OB
，求|
OK
|的最小值（O为坐标原点）．
（3）从圆O外一点M（x1，y1）向该圆引一条切线，切点为T，N（2，3），且有|MT|=|MN|，求|MT|的最小值，并求此时点M的坐标．
已知圆C1：x2+y2=4与直线l：3x+4y-5=0交于A，B两点，若圆C2的圆心在线段AB上，且圆C2与圆C1相切，切点在圆C1的劣弧
AB
上，则圆C2的最大面积为______．
过点P（0，-1）作圆C：x2+y2-2x-4y+4=0的切线
（1）求点P到切点A的距离|PA|；
（2）求切线的方程．
在平面直角坐标系xOy中，已知圆C的方程为x2+y2-8x+15=0，直线l的方程为y=kx-2．
（1）若直线l被圆C所截得弦长为2，求直线l的方程；
（2）若直线l上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，求k的最大值．
从点P（4，5）向圆（x-2）2+y2=4引切线，则圆的切线方程为______．
设P（x，y）是曲线C：
x=-2+cosθ
y=sinθ
(θ为参数，0≤θ＜2π）上任意一点，则
y
x
的取值范围是（　　）
A．[-
3
，
3
]		B．(-∞，-
3
]∪[
3
，+∞)
C．[-
3
3
，
3
3
]		D．(-∞，-
3
3
]∪[
3
3
，+∞)
直线l：y-1=k（x-1）和圆x2+y2-2y=0交点个数是（　　）
A．0B．1
C．2D．个数与k的取值有关
在平面直角坐标系xOy中，圆C的方程为x2+y2-8x+14=0，若直线y=kx-2上至少存在一点，使得以该点为圆心，
2
为半径的圆与圆C有公共点，则k的最大值是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网