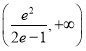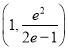题目内容
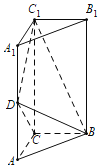
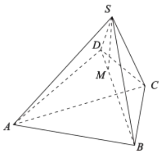
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.

(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将圆柱的一半展开,可知曲线![]() 的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,即可求得曲线
的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,即可求得曲线![]() 的长度.
的长度.
(2)当![]() 时,以底面的圆心O为原点建立空间直角坐标系.写出各个点的坐标,求得平面
时,以底面的圆心O为原点建立空间直角坐标系.写出各个点的坐标,求得平面![]() 的法向量,即可求得点
的法向量,即可求得点![]() 到平面
到平面![]() 的距离.
的距离.
(1)曲线![]() 的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,
的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,
其中![]() ,底面的半圆长为
,底面的半圆长为![]()
∴![]() 的长为
的长为![]()
(2)当![]() 时,建立如图所示的空间直角坐标系:
时,建立如图所示的空间直角坐标系:

则有![]() 、
、![]() 、
、![]() 、
、![]() ,
,
所以![]() 、
、![]() 、
、![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则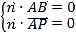 ,代入可得
,代入可得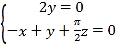 ,
,
令![]() ,得
,得![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为 .
.

【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
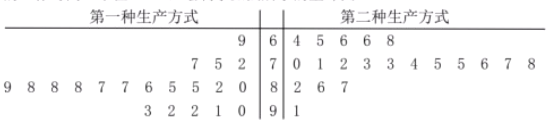
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表,再根据列联表,能否有99.9%的把握认为两种生产方式的效率有差异?
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
附: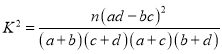 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?