题目内容
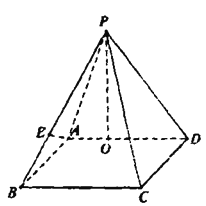
【题目】如图，在直三棱柱
中，
是等腰直角三角形，
，
，点D是侧棱
上的一点.
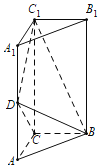
（1）证明：当点D是的中点时，
平面BCD；
（2）若二面角
的余弦值为
求二面角
的余弦值.
【答案】（1）证明见解析；（2）
.
【解析】
(1)分别证明
与
即可.
(2) 以
为坐标原点,分别以射线CA,CB,
为x轴,y轴,z轴的非负半轴建立空间直角坐标系.设
,利用二面角
的余弦值为
求得
,再利用空间向量求解二面角的方法求解二面角
的余弦值即可.
（1）
平面ABC,
平面ABC
又
,
平面
,
平面
平面
,
平面DCB,
平面DCB
平面DCB
（2）
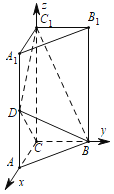
以为坐标原点,分别以射线CA,CB,为x轴,y轴,z轴的非负半轴建立空间直角坐标系.设,
,
,
,
,
设
为平面
的法向量,则
,
设
则有
,
.此时
是平面
的法向量,则
,
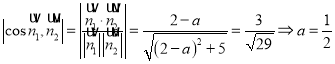因为
是平面
的法向量,则
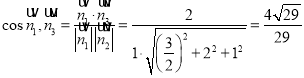
则二面角的余弦值是
【题目】某高校进行自主招生测试，报考学生有500人，其中男生300人，女生200人，为了研究学生的成绩是否与性别有关，现采用分层抽样的方法，从中抽取了100名学生，先统计了他们测试的分数，然后按性别分为男、女两组，再将两组学生的分数分成4组：
，
，
，
分别加以统计，得到如图所示的频率分布直方图.
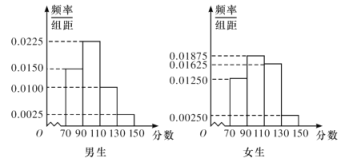
（Ⅰ）根据频率分布直方图可以估计女生测试成绩的平均值为103.5，请你估计男生测试成绩的平均值，由此推断男、女生测试成绩的平均水平的高低；
（Ⅱ）若规定分数不小于110分的学生为“优秀生”，请你根据已知条件完成
列联表，并判断是否有
的把握认为“优秀生与性别有关”？
优秀生 | 非优秀生 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考公式：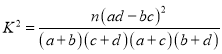
，
.
参考数据：
P（ | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】甲、乙两班举行数学知识竞赛，参赛学生的竞赛得分统计结果如下表：
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论：
①甲、乙两班学生的平均成绩相同；
②乙班优秀的人数少于甲班优秀的人数（竞赛得分
分为优秀）；
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多；
④乙班成绩波动比甲班小.
其中正确结论有（ ）
A.1个B.2个C.3个D.4个
