题目内容
对于定义域为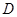 的函数
的函数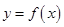 和常数
和常数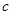 ,若对任意正实数
,若对任意正实数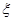 ,
,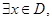 使得
使得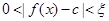 恒成立,则称函数
恒成立,则称函数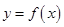 为“敛
为“敛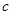 函数”.现给出如下函数:
函数”.现给出如下函数:
①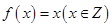 ; ②
; ②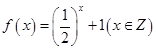 ;
;
③ 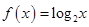 ; ④
; ④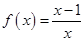 .
.
其中为“敛1函数”的有
| A.①② | B.③④ | C.②③④ | D.①②③ |
C
解析试题分析:根据题意,对于定义域为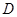 的函数
的函数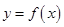 和常数
和常数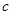 ,若对任意正实数
,若对任意正实数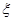 ,
,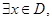 使得
使得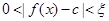 恒成立,则称函数
恒成立,则称函数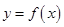 为“敛
为“敛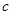 函数”.那么对于
函数”.那么对于
①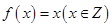 ;由于函数递增,那么不会存在一个正数
;由于函数递增,那么不会存在一个正数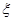 ,满足不等式。
,满足不等式。
②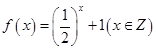 ;当x>0,c=2,那么存在x,满足题意,成立。
;当x>0,c=2,那么存在x,满足题意,成立。
③ 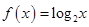 ;对于1<x<2,令c=1,,时符号题意。
;对于1<x<2,令c=1,,时符号题意。
④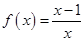 .=1-
.=1-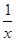 ,x>1,c=3,则可知满足题意。故选C.
,x>1,c=3,则可知满足题意。故选C.
考点:新定义,敛 函数
函数
点评:该试题有创新性,理解概念和运用概念,是解决试题的关键。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
已知 是奇函数,当
是奇函数,当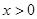 时,
时, 则
则 时,
时, ( )
( )
| A.1 | B.3 | C.-3 | D.-1 |
已知 是定义在
是定义在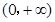 上的单调函数,且对任意的
上的单调函数,且对任意的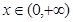 ,都有
,都有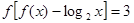 ,则方程
,则方程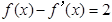 的解所在的区间是 ( )
的解所在的区间是 ( )
A.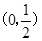  | B.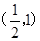 | C.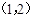 | D.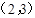 |
判断下列各组中的两个函数是同一函数的为( )
(1) ,
, ;
;
(2) ,
, ;
;
(3) ,
, ;
;
(4) ,
, .
.
| A.(1),(4) | B.(2),(3) | C.(1) | D.(3) |
已知函数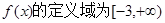 ,且
,且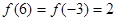 .
.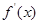 为
为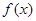 的导函数,
的导函数,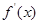 的图像如右图所示.若正数
的图像如右图所示.若正数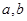 满足
满足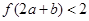 ,则
,则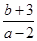 的取值范围是( )
的取值范围是( )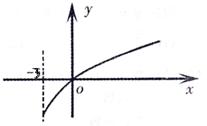
A. | B.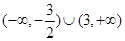 | C.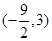 | D.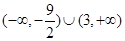 |
下列两个函数为相等函数的是( )
A.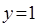 与 与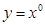 |
B.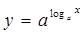 与 与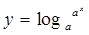 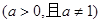 |
C.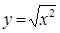 与 与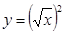 |
D.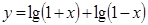 与 与 |
函数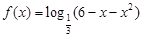 的单调递增区间是
的单调递增区间是
A. | B. | C. | D. |
若定义 上的函数
上的函数 满足:对于任意
满足:对于任意

 且当
且当 时有
时有 ,若
,若 的最大值、最小值分别为M,N,M+N等于( )
的最大值、最小值分别为M,N,M+N等于( )
| A.2011 | B.2012 | C.4022 | D.4024 |
 的函数
的函数 ,若存在非零实数
,若存在非零实数 ,使函数
,使函数 和
和 上均有零点,则称
上均有零点,则称


