题目内容
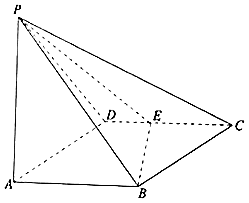
【题目】如图,已知四棱锥S﹣ABCD中,SA⊥平面ABCD,∠ABC=∠BCD=90°,且SA=AB=BC=2CD=2,E是边SB的中点. 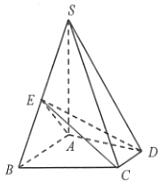
(1)求证:CE∥平面SAD;
(2)求二面角D﹣EC﹣B的余弦值大小.
【答案】
(1)证明:取SA中点F,连结EF,FD,
∵E是边SB的中点,
∴EF∥AB,且EF= ![]() AB,
AB,
又∵∠ABC=∠BCD=90°,
∴AB∥CD,
又∵AB=2CD,且EF=CD,
∴四边形EFDC是平行四边形,
∴FD∥EC,
又FD平面SAD,CE平面SAD,
∴CE∥面SAD
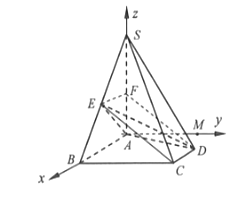
(2)解:在底面内过点A作直线AM∥BC,则AB⊥AM,
又SA⊥平面ABCD,
以AB,AM,AS所在直线分别为x,y,z轴,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(2,2,0),D(1,2,0),D(1,2,0),E(1,0,1),
则 ![]() =(0,2,0),
=(0,2,0), ![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(﹣1,0,),
=(﹣1,0,), ![]() =(﹣1,﹣2,1),
=(﹣1,﹣2,1),
设面BCE的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 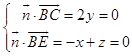 ,取x=1,得
,取x=1,得 ![]() =(1,0,1),
=(1,0,1),
同理求得面DEC的一个法向量为 ![]() =(0,1,2),
=(0,1,2),
cos< ![]() >=
>= ![]() =
= ![]() ,
,
由图可知二面角D﹣EC﹣B是钝二面角,
∴二面角D﹣EC﹣B的余弦值为﹣ ![]() .
.
【解析】(1)取SA中点F,连结EF,FD,推导出四边形EFDC是平行四边形,由此能证明CE∥面SAD.(2)在底面内过点A作直线AM∥BC,则AB⊥AM,以AB,AM,AS所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角D﹣EC﹣B的余弦值.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).

 名校课堂系列答案
名校课堂系列答案【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n的值;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级不相同的概率.
【题目】某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
分组 | 频数 | 频率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合计 | 100 | d |

(1)根据下面的频率分布表和频率分布直方图,求出a+d和b+c的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?