题目内容
【题目】(本小题满分10分)[选修4-5:不等式选讲]
已知函数![]() =|x-a|+
=|x-a|+![]() (a≠0)
(a≠0)
(1)若不等式![]() -
-![]() ≤1恒成立,求实数m的最大值;
≤1恒成立,求实数m的最大值;
(2)当a<![]() 时,函数g(x)=
时,函数g(x)=![]() +|2x-1|有零点,求实数a的取值范围
+|2x-1|有零点,求实数a的取值范围
【答案】(1)1.
(2) [ -![]() ,0 ).
,0 ).
【解析】分析:第一问首先根据题中所给的函数解析式,将相应的变量代入可得结果,之后应用绝对值不等式的性质得到其差值不超过![]() ,这就得到| m |≤1,解出范围从而求得其最大值,第二问解题的方向就是向最小值靠拢,应用最小值小于零,从而求得参数所满足的条件,求得结果.
,这就得到| m |≤1,解出范围从而求得其最大值,第二问解题的方向就是向最小值靠拢,应用最小值小于零,从而求得参数所满足的条件,求得结果.
详解:(Ⅰ) ∵ f (x) =|x-a|+![]() ,∴f(x+m)=|x+m-a|+
,∴f(x+m)=|x+m-a|+![]() ,
,
∴f(x)-f(x+m)=|x-a|-|x+m-a|≤| m | ,
∴| m |≤1 , ∴-1≤ m ≤1 , ∴ 实数 m 的最大值为 1 ;
( Ⅱ )当 a <![]() 时,g(x)=f(x)+|2x -1|=|x-a|+|2x-1|+
时,g(x)=f(x)+|2x -1|=|x-a|+|2x-1|+![]()
=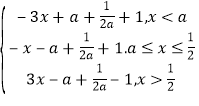
∴ g(x)min =g(![]() )=
)=![]() -a+
-a+![]() =
=![]() ≤0 ,
≤0 ,
∴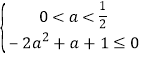 或
或![]() , ∴-
, ∴-![]() ≤a≤0,
≤a≤0,
∴ 实数 a 的取值范围是 [ -![]() ,0 ).
,0 ).

练习册系列答案
相关题目