题目内容
3．已知函数f（x）=loga（2x+b-1）的部分图象如图所示，则a，b所满足的关系是（ ）
| A． | 0＜b-1＜a＜1 | B． | 0＜a-1＜b＜1 | C． | 0＜b＜a-1＜1 | D． | 0＜a-1＜b-1＜1 |
分析 根据图象性质得出a＞1，-1＜f（0）＜0，即-1＜logab＜0，解对数不等式即可．
解答 解：函数f（x）=loga（2x+b-1）的部分图象如图所示，
∴函数单调递增，
得出a＞1
-1＜f（0）＜0，
即-1＜logab＜0，
解不等式得出：0＜a-1＜b＜1，
故选：B
点评 本题考查了有关的对数函数的性质，图象，对数不等式的求解，关键是确定底数的范围，利用单调性转化问题，难度不大，属于中档题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13．在二项式（x2-$\frac{1}{x}$）5的展开式中，含x7的项的系数为（ ）
| A． | -10 | B． | 10 | C． | -5 | D． | 5 |
14．设变量x，y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥-2\end{array}\right.$则z=|x-3y|的取值范围为（ ）
| A． | [2，8] | B． | [0，8] | C． | [4，8] | D． | [0，4] |
11．如图，若N=2015时，则输出的数等于（ ）
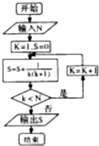
| A． | $\frac{2015}{2014}$ | B． | $\frac{2014}{2015}$ | C． | $\frac{2016}{2015}$ | D． | $\frac{2015}{2016}$ |
18．设△ABC的内角A，B，C所对的边a，b，c成等比数列，则$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$的取值范围是（ ）
| A． | （0，+∞） | B． | $（{\frac{{\sqrt{5}-1}}{2}，+∞}）$ | C． | $（{0，\frac{{\sqrt{5}+1}}{2}}）$ | D． | $（{\frac{{\sqrt{5}-1}}{2}，\frac{{\sqrt{5}+1}}{2}}）$ |
8．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（x，y）．则“x=-2且y=-4”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
12．已知函数$f（x）=\frac{{sinx+cosx+|{sinx-cosx}|}}{2}$，则下列结论正确的是（ ）
| A． | f（x）是奇函数 | B． | f（x）在$[{0，\frac{π}{2}}]$上递增 | C． | f（x）是周期函数 | D． | f（x）的值域为[-1，1] |
.
时，求函数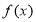
的定义域；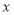
的不等式
的解集是
，求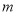
的取值范围.