题目内容
函数

 .
.
(1)当 时,求证:
时,求证: ;
;
(2)在区间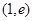 上
上
 恒成立,求实数
恒成立,求实数 的范围。
的范围。
(3)当 时,求证:
时,求证: )
) .
.
(1)根据构造函数利用导数来得到函数的最小值,只要证明最小值大于等于零即可。
(2)
(3)在第一问的基础上,结合 ,放缩法来得到证明。
,放缩法来得到证明。
解析试题分析:解:
(1)明:设
则 ,则
,则 ,即
,即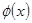 在
在 处取到最小值,
处取到最小值,
则 ,即原结论成立. 4分
,即原结论成立. 4分
(2):由 得
得 即
即 ,另
,另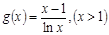 ,
,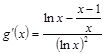
另 ,
,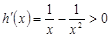 则
则 单调递增,所以
单调递增,所以
因为 ,所以
,所以 ,即
,即 单调递增,则
单调递增,则 的最大值为
的最大值为
所以 的取值范围为
的取值范围为 . 8分
. 8分
(3):由第一问得知 则
则 - 10分
- 10分
则



 13分
13分
考点:函数的单调性与导数的运用
点评:解决的关键是结合导数的符号来判定函数单调性,进而得到最值,并能证明不等式,属于中档题。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,直线x+y=3以及两坐标轴所围成的图形的面积S.
,直线x+y=3以及两坐标轴所围成的图形的面积S.
 ,
, .求函数
.求函数 的单调递减区间;
的单调递减区间; 在
在 上是增函数.
上是增函数.
 的解析式及减区间;
的解析式及减区间; 的最小值。
的最小值。 ,若存在
,若存在 使得
使得 恒成立,则称
恒成立,则称 是
是 的
的 (t为实数)为
(t为实数)为 的一个“下界函数”,
的一个“下界函数”, ,试问函数
,试问函数 是否存在零点,若存在,求出零点个数;
是否存在零点,若存在,求出零点个数; .
. 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围. .
. 在点
在点 处的切线方程;
处的切线方程; ,如果过点
,如果过点 可作曲线
可作曲线

 在点
在点 处的切线与直线
处的切线与直线 垂直,求a的值;
垂直,求a的值;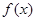 的单调区间;
的单调区间; 满足0<
满足0< 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; ,
,