题目内容
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(1)从中同时摸出两个球,求两球颜色恰好相同的概率;
(2)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
(1) ;(2)
;(2)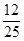 。
。
解析试题分析:由题意知每个球被摸出的机会均等,即为古典概型,问题(1)的基本事件总数为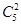 ,两球颜
,两球颜
色恰好相同包括的基本事件个数为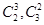 ;问题(2)是有放回的摸取,则基本事件总数为
;问题(2)是有放回的摸取,则基本事件总数为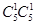 ,两球颜
,两球颜
色恰好不同包括的基本事件个数为 ,然后用古典概型公式求解。
,然后用古典概型公式求解。
(1)摸出两球颜色恰好相同,即两个黑球或两个白球,共有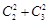 =4(种)可能情况.
=4(种)可能情况.
故所求概率为P=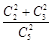 =
=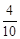 =
= .
.
(2)有放回地摸两次,两球颜色不同,即“先黑后白”或“先白后黑”.
故所求概率为P=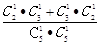 =
= =
=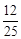 .
.
考点:(1)古典概型的定义及其概率的求法;(2)有放回抽取与无放回抽取的区别。

练习册系列答案
相关题目
 .
.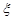 的数学期望和方差.
的数学期望和方差.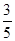 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是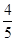 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用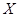 表示张同学答对题的个数,求
表示张同学答对题的个数,求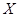 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求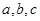 满足
满足 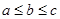 ,则称
,则称 为这三个数的中位数).
为这三个数的中位数).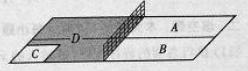 甲上有两个不相交的区域
甲上有两个不相交的区域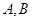 ,乙被划分为两个不相交的区域
,乙被划分为两个不相交的区域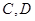 .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在
.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在 上记3分,在
上记3分,在 上记1分,其它情况记0分.对落点在
上记1分,其它情况记0分.对落点在 上的来球,队员小明回球的落点在
上的来球,队员小明回球的落点在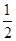 ,在
,在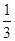 ;对落点在
;对落点在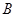 上的来球,小明回球的落点在
上的来球,小明回球的落点在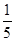 ,在
,在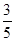 .假设共有两次来球且落在
.假设共有两次来球且落在 的分布列与数学期望.
的分布列与数学期望.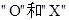 随机地反复出现,每秒钟变化一次,每次变化只出现
随机地反复出现,每秒钟变化一次,每次变化只出现 的概率为p,出现
的概率为p,出现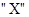 的概率为q,若第k次出现
的概率为q,若第k次出现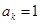 ;出现
;出现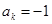 ,令
,令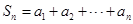 .
.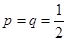 时,求
时,求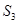 的分布列及数学期望.
的分布列及数学期望.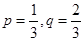 时,求
时,求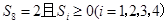 的概率.
的概率.