题目内容
为喜迎马年新春佳节,某商场在正月初六进行抽奖促销活动,当日在该店消费满500元的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有 “马”“上”“有”“钱”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“钱”字球,则停止取球.获奖规则如下:依次取到标有“马”“上”“有”“钱”字的球为一等奖;不分顺序取到标有“马”“上”“有”“钱”字的球,为二等奖;取到的4个球中有标有“马”“上”“有”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为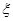 ,求
,求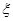 的分布列和数学期望.
的分布列和数学期望.
(1)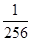 ,
,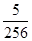 ,
,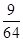 ;(2)详见解析
;(2)详见解析
解析试题分析:(1)首先设“摸到一等奖、二等奖、三等奖”分别为事件A,B,C.有放回地取四次球,相当于四次独立重复试验,且每次试验“马”“上”“有”“钱”四个字出现的概率均为 ,可依据一等奖、二等奖、三等奖各自的条件求出相应的概率值;
,可依据一等奖、二等奖、三等奖各自的条件求出相应的概率值;
(2)设摸球的次数为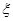 ,则
,则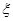 的所有可能取值为1、2、3、4.
的所有可能取值为1、2、3、4.
四次独立重复试验,每次取到“钱”发生的概率为 ,不发生的概率则为
,不发生的概率则为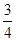 ,根据题意可求
,根据题意可求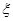 的分布列及数学期望.
的分布列及数学期望.
解:(1)设“摸到一等奖、二等奖、三等奖”分别为事件A,B,C.
则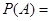
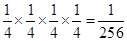 (列式正确,计算错误,扣1分) 2分
(列式正确,计算错误,扣1分) 2分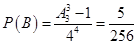 (列式正确,计算错误,扣1分) 4分
(列式正确,计算错误,扣1分) 4分
三等奖情况有:“马,马,上,有”,“马,上,上,有”,“马,上,有”三种情况.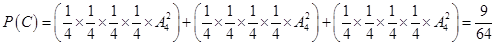 6分
6分
(2)设摸球的次数为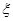 ,则
,则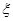 的所有可能取值为1、2、3、4.
的所有可能取值为1、2、3、4.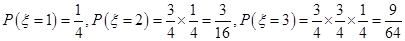
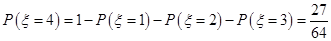 10分
10分
故取球次数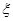 的分布列为:
的分布列为: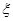
1 2 3 4 P 
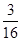
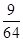
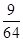
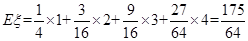 12分
12分
考点:1、独立重复试验;2、离散型随机变量的分布列及数学期望.

计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量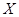 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量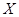 限制,并有如下关系:
限制,并有如下关系:
年入流量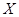 | 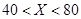 | 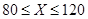 | 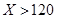 |
| 发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为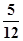 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为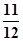 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品. 个,设
个,设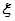 表示其中合格品的个数,求
表示其中合格品的个数,求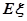 .
.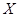 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求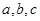 满足
满足 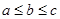 ,则称
,则称 为这三个数的中位数).
为这三个数的中位数).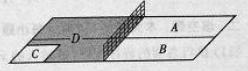 甲上有两个不相交的区域
甲上有两个不相交的区域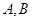 ,乙被划分为两个不相交的区域
,乙被划分为两个不相交的区域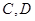 .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在
.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在 上记3分,在
上记3分,在 上记1分,其它情况记0分.对落点在
上记1分,其它情况记0分.对落点在 上的来球,队员小明回球的落点在
上的来球,队员小明回球的落点在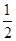 ,在
,在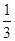 ;对落点在
;对落点在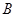 上的来球,小明回球的落点在
上的来球,小明回球的落点在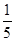 ,在
,在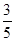 .假设共有两次来球且落在
.假设共有两次来球且落在 的分布列与数学期望.
的分布列与数学期望.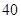 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: 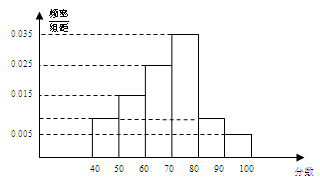
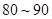 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?