ƒøƒ⁄»ð
£®2011•À≥“«¯∂˛ƒ££©∂‘”⁄∂®“”Ú∑÷±Œ™M£¨Nµƒ∫Ø ˝y=f£®x£©£¨y=g£®x£©£¨πÊ∂®£∫
∫Ø ˝h(x)=
£®1£©»Ù∫Ø ˝f(x)=
£¨g(x)=x2+2x+2£¨x° R£¨«Û∫Ø ˝h£®x£©µƒ»°÷µºØ∫œ£ª
£®2£©»Ùf£®x£©=1£¨g£®x£©=x2+2x+2£¨…ËbnŒ™«˙œþy=h£®x£©‘⁄µ„£®an£¨h£®an£©£©¥¶«–œþµƒ–±¬ £ª∂¯{an} «µ»≤Ó ˝¡–£¨π´≤ÓŒ™1£®n° N*£©£¨µ„P1Œ™÷±œþl£∫2x-y+2=0”Îx÷·µƒΩªµ„£¨µ„Pnµƒ◊¯±ÍŒ™£®an£¨bn£©£Æ«Û÷§£∫
+
+°≠+
£º
£ª
£®3£©»Ùg£®x£©=f£®x+¶¡£©£¨∆‰÷–¶¡ «≥£ ˝£¨«“¶¡° [0£¨2¶–]£¨«ÎŒ £¨ «∑ҥʑ⁄“ª∏ˆ∂®“”ڌ™Rµƒ∫Ø ˝y=f£®x£©º∞“ª∏ˆ¶¡µƒ÷µ£¨ πµ√h£®x£©=cosx£¨»Ù¥Ê‘⁄«Î–¥≥ˆ“ª∏ˆf£®x£©µƒΩ‚Œˆ Ωº∞“ª∏ˆ¶¡µƒ÷µ£¨»Ù≤ª¥Ê‘⁄«ÎÀµ√˜¿Ì”…£Æ
∫Ø ˝h(x)=
|
£®1£©»Ù∫Ø ˝f(x)=
| 1 |
| x+1 |
£®2£©»Ùf£®x£©=1£¨g£®x£©=x2+2x+2£¨…ËbnŒ™«˙œþy=h£®x£©‘⁄µ„£®an£¨h£®an£©£©¥¶«–œþµƒ–±¬ £ª∂¯{an} «µ»≤Ó ˝¡–£¨π´≤ÓŒ™1£®n° N*£©£¨µ„P1Œ™÷±œþl£∫2x-y+2=0”Îx÷·µƒΩªµ„£¨µ„Pnµƒ◊¯±ÍŒ™£®an£¨bn£©£Æ«Û÷§£∫
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
£®3£©»Ùg£®x£©=f£®x+¶¡£©£¨∆‰÷–¶¡ «≥£ ˝£¨«“¶¡° [0£¨2¶–]£¨«ÎŒ £¨ «∑ҥʑ⁄“ª∏ˆ∂®“”ڌ™Rµƒ∫Ø ˝y=f£®x£©º∞“ª∏ˆ¶¡µƒ÷µ£¨ πµ√h£®x£©=cosx£¨»Ù¥Ê‘⁄«Î–¥≥ˆ“ª∏ˆf£®x£©µƒΩ‚Œˆ Ωº∞“ª∏ˆ¶¡µƒ÷µ£¨»Ù≤ª¥Ê‘⁄«ÎÀµ√˜¿Ì”…£Æ
∑÷Œˆ£∫£®1£©”…∫Ø ˝f(x)=
£¨g(x)=x2+2x+2£¨x° R£¨ø…µ√M={x|x°Ÿ-1}£¨N=R£Æ¥”∂¯h(x)=
£Æ”…¥ÀƒÐ«Û≥ˆ∫Ø ˝h£®x£©µƒ»°÷µºØ∫œ£Æ
£®2£©”…h£®x£©=x2+2x+2£¨÷™h'£®x£©=2x+2£¨À˘“‘bn=g'£®an£©=2an+2£¨”…µ„Pn£®an£¨bn£©‘⁄÷±œþl…œ£¨«“a1=-1£¨”÷{an} «µ»≤Ó ˝¡–£¨π´≤ÓŒ™1£¨÷™an=n-2£¨bn=2n-2π Pn£®n-2£¨2n-2£©£¨”…¥ÀƒÐπª÷§√˜
+
+°≠+
£º
£Æ£®3£©”…∫Ø ˝y=f£®x£©µƒ∂®“”ڌ™R£¨µ√g£®x£©=f£®x+a£©µƒ∂®“”ڌ™R£ÆÀ˘“‘£¨∂‘”⁄»Œ“‚x° R£¨∂º”–h£®x£©=f£®x£©•g£®x£©
º¥∂‘”⁄»Œ“‚x° R£¨∂º”–cosx=f£®x£©•f£®x+a£©£¨À˘“‘£¨¡Óf(x)=
cos(
-
)£¨«“¶¡=¶–£¨º¥ø…£Æ
| 1 |
| x+1 |
|
£®2£©”…h£®x£©=x2+2x+2£¨÷™h'£®x£©=2x+2£¨À˘“‘bn=g'£®an£©=2an+2£¨”…µ„Pn£®an£¨bn£©‘⁄÷±œþl…œ£¨«“a1=-1£¨”÷{an} «µ»≤Ó ˝¡–£¨π´≤ÓŒ™1£¨÷™an=n-2£¨bn=2n-2π Pn£®n-2£¨2n-2£©£¨”…¥ÀƒÐπª÷§√˜
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
º¥∂‘”⁄»Œ“‚x° R£¨∂º”–cosx=f£®x£©•f£®x+a£©£¨À˘“‘£¨¡Óf(x)=
| 2 |
| x |
| 2 |
| ¶– |
| 4 |
Ω‚¥£∫Ω‚£∫£®1£©”…∫Ø ˝f(x)=
£¨g(x)=x2+2x+2£¨x° Rø…µ√M={x|x°Ÿ-1}£¨N=R
¥”∂¯h(x)=
µ±x£æ-1 ±£¨h(x)=
=
=x+1+
°ð2
µ±x£º-1 ±£¨h(x)=
=
=-(-x-1+
)°Ð-2
À˘“‘h£®x£©µƒ»°÷µºØ∫œŒ™{y|y°Ð-2£¨ªÚy°ð2ªÚy=1}°≠£Æ£®5∑÷£©
£®2£©“◊÷™h£®x£©=x2+2x+2£¨
À˘“‘h'£®x£©=2x+2À˘“‘bn=g'£®an£©=2an+2
œ‘»ªµ„Pn£®an£¨bn£©‘⁄÷±œþl…œ£¨«“a1=-1£¨
”÷{an} «µ»≤Ó ˝¡–£¨π´≤ÓŒ™1
À˘“‘an=n-2£¨bn=2n-2π Pn£®n-2£¨2n-2£©£¨”÷P1£®-1£¨0£©
À˘“‘|P1Pn|=
(n-1)(n°ð2)
À˘“‘
+
+°≠+
=
[1+
+
+°≠+
]£º
[1+
+
+°≠+
]
=
[1+1-
]£º
°≠..£®8∑÷£©
£®3£©”…∫Ø ˝y=f£®x£©µƒ∂®“”ڌ™R£¨
µ√g£®x£©=f£®x+a£©µƒ∂®“”ڌ™R£¨
À˘“‘£¨∂‘”⁄»Œ“‚x° R£¨∂º”–h£®x£©=f£®x£©•g£®x£©
º¥∂‘”⁄»Œ“‚x° R£¨∂º”–cosx=f£®x£©•f£®x+a£©
À˘“‘£¨Œ“√«øº¬«Ω´cosx∑÷Ω‚≥…¡Ω∏ˆ∫Ø ˝µƒ≥Àª˝£¨
∂¯«“’‚¡Ω∏ˆ∫Ø ˝ªπø…“‘Õ®π˝∆Ω“∆œýª•◊™ªØ
cosx=cos2
-sin2
=(cos
+sin
)(cos
-sin
)
=
cos(
-
)•
cos(
+
)
À˘“‘£¨¡Óf(x)=
cos(
-
)£¨
«“¶¡=¶–£¨º¥ø… °≠..£®13∑÷£©
”÷cosx=1-2sin2
=(1+
sin
)(1-
sin
)
À˘“‘£¨¡Óf(x)=1+
sin
£¨
«“¶¡=2¶–£¨º¥ø…£®¥∞∏≤ªŒ®“ª£©
| 1 |
| x+1 |
¥”∂¯h(x)=
|
µ±x£æ-1 ±£¨h(x)=
| x2+2x+2 |
| x+1 |
| (x+1)2+1 |
| x+1 |
| 1 |
| x+1 |
µ±x£º-1 ±£¨h(x)=
| x2+2x+2 |
| x+1 |
| (x+1)2+1 |
| x+1 |
| 1 |
| -x-1 |
À˘“‘h£®x£©µƒ»°÷µºØ∫œŒ™{y|y°Ð-2£¨ªÚy°ð2ªÚy=1}°≠£Æ£®5∑÷£©
£®2£©“◊÷™h£®x£©=x2+2x+2£¨
À˘“‘h'£®x£©=2x+2À˘“‘bn=g'£®an£©=2an+2
œ‘»ªµ„Pn£®an£¨bn£©‘⁄÷±œþl…œ£¨«“a1=-1£¨
”÷{an} «µ»≤Ó ˝¡–£¨π´≤ÓŒ™1
À˘“‘an=n-2£¨bn=2n-2π Pn£®n-2£¨2n-2£©£¨”÷P1£®-1£¨0£©
À˘“‘|P1Pn|=
| 5 |
À˘“‘
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 1 |
| 5 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (n-1)2 |
| 1 |
| 5 |
| 1 |
| 1•2 |
| 1 |
| 2•3 |
| 1 |
| (n-2)(n-1) |
=
| 1 |
| 5 |
| 1 |
| n-1 |
| 2 |
| 5 |
£®3£©”…∫Ø ˝y=f£®x£©µƒ∂®“”ڌ™R£¨
µ√g£®x£©=f£®x+a£©µƒ∂®“”ڌ™R£¨
À˘“‘£¨∂‘”⁄»Œ“‚x° R£¨∂º”–h£®x£©=f£®x£©•g£®x£©
º¥∂‘”⁄»Œ“‚x° R£¨∂º”–cosx=f£®x£©•f£®x+a£©
À˘“‘£¨Œ“√«øº¬«Ω´cosx∑÷Ω‚≥…¡Ω∏ˆ∫Ø ˝µƒ≥Àª˝£¨
∂¯«“’‚¡Ω∏ˆ∫Ø ˝ªπø…“‘Õ®π˝∆Ω“∆œýª•◊™ªØ
cosx=cos2
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=
| 2 |
| x |
| 2 |
| ¶– |
| 4 |
| 2 |
| x |
| 2 |
| ¶– |
| 4 |
À˘“‘£¨¡Óf(x)=
| 2 |
| x |
| 2 |
| ¶– |
| 4 |
«“¶¡=¶–£¨º¥ø… °≠..£®13∑÷£©
”÷cosx=1-2sin2
| x |
| 2 |
| 2 |
| x |
| 2 |
| 2 |
| x |
| 2 |
À˘“‘£¨¡Óf(x)=1+
| 2 |
| x |
| 2 |
«“¶¡=2¶–£¨º¥ø…£®¥∞∏≤ªŒ®“ª£©
µ„∆¿£∫±æ ˝¡–”Î≤ªµ» Ωµƒ◊€∫œ£¨Ω·∫œ»˝Ω«∫Ø ˝µƒ–‘÷ µƒ¥¶¿ÌŒ £¨∂‘ ˝—ßÀºŒ¨µƒ“™«Û±»Ωœ∏þ£¨”–“ª∂®µƒÃΩÀ˜–‘£Æ◊€∫œ–‘«ø£¨ƒ—∂»¥Û£¨“◊≥ˆ¥Ì£ÆΩ‚Ã‚ ±“™»œ’Ê…Û£¨◊¢“‚»˝Ω«∫Ø ˝–‘÷ µƒ¡ÈªÓ‘À”√£Æ

¡∑œ∞≤·œµ¡–¥∞∏
 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
œýπÿƒø
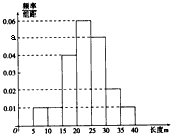 £®2011•À≥“«¯∂˛ƒ££©ƒ≥√Þ∑ƒ≥ߌ™¡ÀΩ‚“ª≈˙√Þª®µƒ÷ ¡ø£¨¥”÷–Àʪ˙≥È≤‚100∏˘√Þª®œÀŒ¨µƒ≥§∂»£®√Þª®œÀŒ¨µƒ≥§∂» «√Þª®÷ ¡øµƒ÷ÿ“™÷∏±Í£©£ÆÀ˘µ√ ˝æðæ˘‘⁄«¯º‰[5£¨40]÷–£¨∆‰∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ 棨”…Õº÷– ˝æðø…÷™a=
£®2011•À≥“«¯∂˛ƒ££©ƒ≥√Þ∑ƒ≥ߌ™¡ÀΩ‚“ª≈˙√Þª®µƒ÷ ¡ø£¨¥”÷–Àʪ˙≥È≤‚100∏˘√Þª®œÀŒ¨µƒ≥§∂»£®√Þª®œÀŒ¨µƒ≥§∂» «√Þª®÷ ¡øµƒ÷ÿ“™÷∏±Í£©£ÆÀ˘µ√ ˝æðæ˘‘⁄«¯º‰[5£¨40]÷–£¨∆‰∆µ¬ ∑÷≤º÷±∑ΩÕº»ÁÕºÀ˘ 棨”…Õº÷– ˝æðø…÷™a=