题目内容
（（本小题满分12分）
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于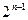
＋1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2) 若规定n≤3, 求某人的过关数ξ的期望.
一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于
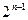＋1 (n∈N*), 则算过关.(1)求在这项游戏中第三关过关的概率是多少?
(2) 若规定n≤3, 求某人的过关数ξ的期望.
解(1)设第三关不过关事件为A, 则第三关过关事件为 .由题设可知: 事件A是指第三关出现点数之和没有大于5.因为第三关出现点数之和为3,4, 5的次数分别为1,3,6知:
P(A)= = , ∴P()=1－ = .
(2)设第一关不过关的事件为B, 第二关不过关的事件为C.依题意,
得P(B)= = , P()=P( C) = = , P()=1－ = .
∵n≤3, ∴ξ的取值分别为0,1,2,3
∴P(ξ="0)=P(B)=" , P(ξ="1)=P(·C" )= ×=
P(ξ="2)=" P(··A) = ×× = P(ξ="3)=" P(··) = ××=
故ξ的分布列:
Eξ=0×＋1×＋2×＋3×=
P(A)= = , ∴P()=1－ = .
(2)设第一关不过关的事件为B, 第二关不过关的事件为C.依题意,
得P(B)= = , P()=P( C) = = , P()=1－ = .
∵n≤3, ∴ξ的取值分别为0,1,2,3
∴P(ξ="0)=P(B)=" , P(ξ="1)=P(·C" )= ×=
P(ξ="2)=" P(··A) = ×× = P(ξ="3)=" P(··) = ××=
故ξ的分布列:
| ξ | 0 | 1 | 2 | 3 |
| P | ||||
| ξ | 0 | 1 | 2 | 3 |
| P | ||||
| ξ | 0 | 1 | 2 | 3 |
| P |
略
练习册系列答案
相关题目
的分布列。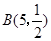
，则P(X=1)= ▲ ．（用数字作答）
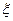，求
中样本橘子树产量的分组区间为[5，15），[15，25），[25，35），[35，45），[45，55），由此得到表1和图1的所示内容，其中表1是施用A种肥料后橘子树产量的频数分布表，图1是施用B种肥料后橘子树产量的频率分布直方图．
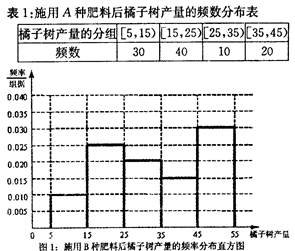
0分)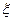 
表示取出球的最大号码，求
