题目内容
设△ABC的内角A,B,C的对边分别为a,b,c,且A=60°,c=3b.求:
(1)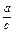 的值;
的值;
(2)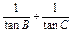 的值.
的值.
(1)
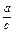 的值;
的值;(2)
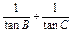 的值.
的值.(1)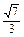 (2)
(2)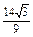
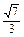 (2)
(2)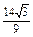
(1)由余弦定理得
a2=b2+c2-2bccosA
=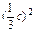 +c2-2·
+c2-2·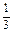 c·c·
c·c·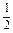 =
=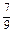 c2,
c2,
故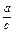 =
=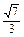 .
.
(2)方法一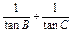 =
=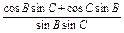
=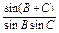 =
=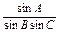 ,
,
由正弦定理和(1)的结论得
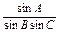 =
=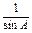 ·
· 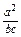 =
=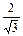 ·
·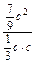 =
=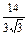 =
=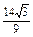 .
.
故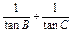 =
=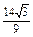 .
.
方法二 由余弦定理及(1)的结论有
cosB=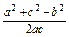 =
=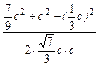 =
=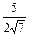 ,
,
故sinB= =
=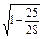 =
=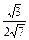 .
.
同理可得
cosC=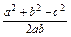 =
=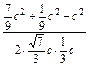 =-
=-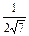 ,
,
sinC=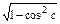 =
=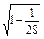 =
=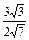 .
.
从而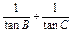 =
= +
+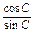
=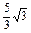 -
-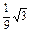 =
=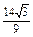 .
.
a2=b2+c2-2bccosA
=
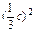 +c2-2·
+c2-2·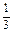 c·c·
c·c·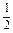 =
=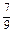 c2,
c2,故
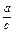 =
=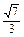 .
.(2)方法一
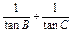 =
=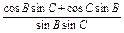
=
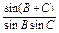 =
=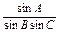 ,
, 由正弦定理和(1)的结论得
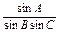 =
=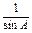 ·
· 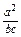 =
=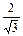 ·
·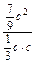 =
=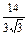 =
=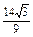 .
.故
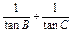 =
=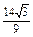 .
.方法二 由余弦定理及(1)的结论有
cosB=
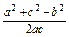 =
=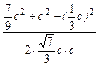 =
=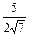 ,
,故sinB=
 =
=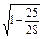 =
=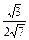 .
.同理可得
cosC=
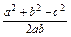 =
=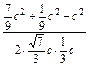 =-
=-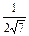 ,
,sinC=
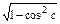 =
=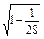 =
=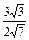 .
.从而
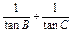 =
= +
+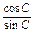
=
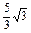 -
-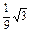 =
=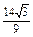 .
.
练习册系列答案
相关题目
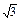 b,判断△ABC的形状.
b,判断△ABC的形状.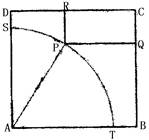
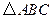 中,
中,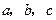 分别是角
分别是角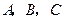 的对边,设
的对边,设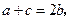
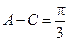 ,求
,求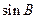 的值.
的值.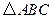 中,已知
中,已知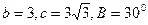 ,求角
,求角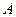 ,角
,角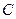 和边
和边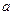 .
.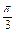 ,求角C的大小;
,求角C的大小;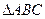 中,角
中,角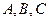 所对的边分别为
所对的边分别为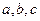 ,且满足
,且满足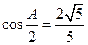 ,
,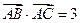 .(1)求
.(1)求 ,求
,求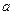 的值.
的值.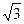 cos(A+B)=0,.当
cos(A+B)=0,.当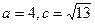 ,求△ABC的面积。
,求△ABC的面积。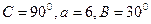 ,则
,则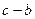 等于( )
等于( )