题目内容
在△ABC中,a,b,c分别为角A、B、C的对边,设f(x)=a2x2-(a2-b2)x-4c2.
(1)f(1)=0且B-C=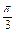 ,求角C的大小;
,求角C的大小;
(2)若f(2)=0,求角C的取值范围.
(1)f(1)=0且B-C=
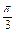 ,求角C的大小;
,求角C的大小;(2)若f(2)=0,求角C的取值范围.
(1)C=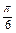 (2)0<C≤
(2)0<C≤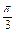
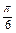 (2)0<C≤
(2)0<C≤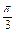
(1)∵f(1)=0,∴a2-(a2-b2)-4c2=0,
∴b2=4c2,∴b=2c,∴sinB=2sinC,
又B-C=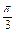 .∴sin(C+
.∴sin(C+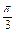 )=2sinC,
)=2sinC,
∴sinC·cos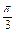 +cosC·sin
+cosC·sin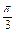 =2sinC,
=2sinC,
∴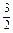 sinC-
sinC-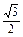 cosC=0,∴sin(C-
cosC=0,∴sin(C-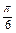 )=0,
)=0,
又∵-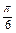 <C-
<C-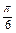 <
<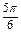 ,∴C=
,∴C=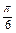 .
.
(2)若f(2)=0,则4a2-2(a2-b2)-4c2=0,
∴a2+b2=2c2,∴cosC=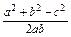 =
=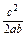 ,
,
又2c2=a2+b2≥2ab,∴ab≤c2,∴cosC≥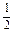 ,
,
又∵C∈(0,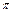 ),∴0<C≤
),∴0<C≤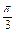 .
.
∴b2=4c2,∴b=2c,∴sinB=2sinC,
又B-C=
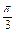 .∴sin(C+
.∴sin(C+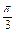 )=2sinC,
)=2sinC,∴sinC·cos
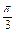 +cosC·sin
+cosC·sin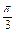 =2sinC,
=2sinC,∴
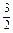 sinC-
sinC-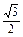 cosC=0,∴sin(C-
cosC=0,∴sin(C-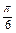 )=0,
)=0,又∵-
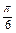 <C-
<C-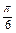 <
<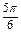 ,∴C=
,∴C=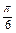 .
.(2)若f(2)=0,则4a2-2(a2-b2)-4c2=0,
∴a2+b2=2c2,∴cosC=
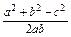 =
=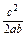 ,
,又2c2=a2+b2≥2ab,∴ab≤c2,∴cosC≥
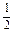 ,
,又∵C∈(0,
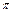 ),∴0<C≤
),∴0<C≤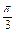 .
.
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
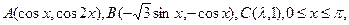 若△ABC的重心在
若△ABC的重心在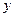 轴负半轴上,求实数
轴负半轴上,求实数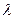 的取值范围.
的取值范围.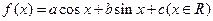 的图象经过点
的图象经过点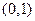 ,
,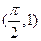 ,当
,当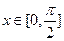 时,恒有
时,恒有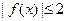 ,求实数
,求实数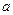 的取值范围
的取值范围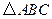 中,已知
中,已知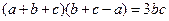 ,且
,且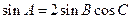 ,试确定
,试确定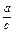 的值;
的值;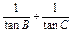 的值.
的值.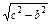 x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10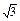 ,c=7.
,c=7.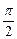 ,试求∠A、∠B、∠C的值.
,试求∠A、∠B、∠C的值.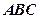 中,已知
中,已知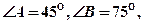 点
点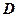 在
在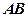 上,且
上,且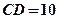 .若点
.若点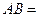 。
。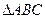 中,角
中,角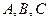 的对边分别为
的对边分别为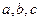 ,且
,且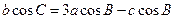 。
。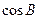 的值。(2)若
的值。(2)若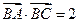 ,且
,且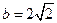 ,求a和c的值。
,求a和c的值。