题目内容
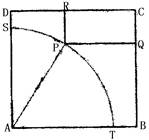
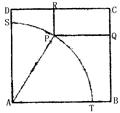
如图,四边形ABCD是一个边长为100米的正方形地皮,其中ATPS是一半径为90米的扇形小山,其余部分都是平地,P是弧TS上一点,现有一位开发商想在平地上建造一个两边落在BC与CD上的长方形停车场PQCR.
(Ⅰ)若∠PAT=θ,试写出四边形RPQC的面积S关于θ
的函数表达式,并写出定义域;
(Ⅱ)试求停车场的面积最大值。
|
(Ⅰ)若∠PAT=θ,试写出四边形RPQC的面积S关于θ
的函数表达式,并写出定义域;
(Ⅱ)试求停车场的面积最大值。
(1) =10000-
=10000-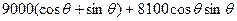
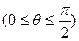
(2)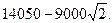
 =10000-
=10000-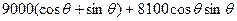
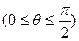
(2)
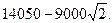
(Ⅰ)延长RP交AB于M,设∠PAB=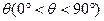 ,则
,则
AM =90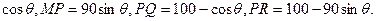
∴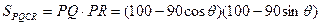
=10000-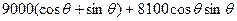
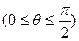
(Ⅱ)设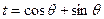 ∵
∵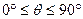 ∴
∴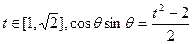
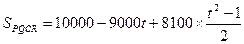

∴当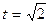 时,SPQCR有最大值
时,SPQCR有最大值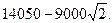
答:长方形停车场PQCR面积的最磊值为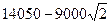 平方米。
平方米。
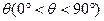 ,则
,则AM =90
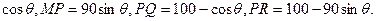
∴
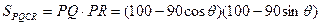
=10000-
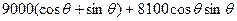
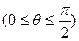
|
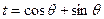 ∵
∵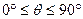 ∴
∴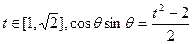
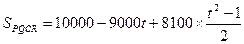

∴当
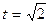 时,SPQCR有最大值
时,SPQCR有最大值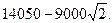
答:长方形停车场PQCR面积的最磊值为
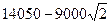 平方米。
平方米。
练习册系列答案
相关题目
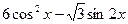
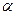 满足
满足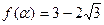 ,求tan
,求tan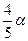 的值。(4分)
的值。(4分)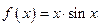 ,若
,若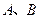 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则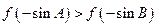

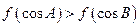

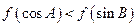

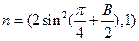 ,m⊥n,
,m⊥n,
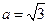 ,b=1,求c的值.
,b=1,求c的值.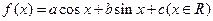 的图象经过点
的图象经过点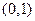 ,
,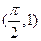 ,当
,当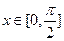 时,恒有
时,恒有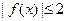 ,求实数
,求实数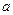 的取值范围
的取值范围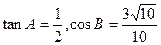
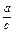 的值;
的值;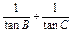 的值.
的值.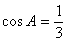 .
.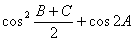 的值;
的值;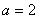 ,
,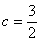 ,求∠C和ΔABC的面积.
,求∠C和ΔABC的面积.