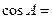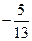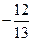题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,并且a2=b(b+c).
(1)求证:A=2B;
(2)若a=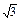 b,判断△ABC的形状.
b,判断△ABC的形状.
(1)求证:A=2B;
(2)若a=
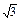 b,判断△ABC的形状.
b,判断△ABC的形状.(1)证明见解析(2)
(1)证明 因为a2=b(b+c),即a2=b2+bc,
所以在△ABC中,由余弦定理可得,
cosB=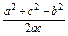 =
=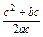 =
=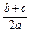
=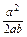 =
=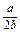 =
=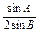 ,
,
所以sinA=sin2B,故A=2B.
(2)解 因为a=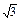 b,所以
b,所以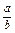 =
=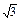 ,
,
由a2=b(b+c)可得c=2b,
cosB=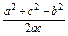 =
=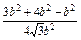 =
=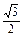 ,
,
所以B=30°,A=2B=60°,C=90°.
所以△ABC为直角三角形.
所以在△ABC中,由余弦定理可得,
cosB=
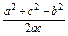 =
=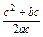 =
=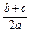
=
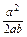 =
=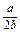 =
=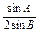 ,
,所以sinA=sin2B,故A=2B.
(2)解 因为a=
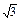 b,所以
b,所以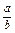 =
=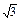 ,
,由a2=b(b+c)可得c=2b,
cosB=
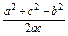 =
=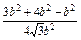 =
=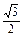 ,
,所以B=30°,A=2B=60°,C=90°.
所以△ABC为直角三角形.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
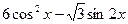
 满足
满足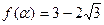 ,求tan
,求tan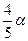 的值。(4分)
的值。(4分)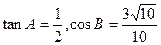
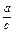 的值;
的值;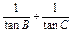 的值.
的值.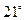 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成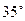 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
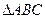 中,角
中,角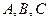 的对边分别为
的对边分别为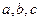 ,且
,且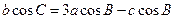 。
。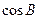 的值。(2)若
的值。(2)若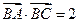 ,且
,且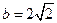 ,求a和c的值。
,求a和c的值。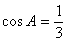 .
.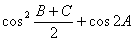 的值;
的值;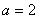 ,
,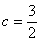 ,求∠C和ΔABC的面积.
,求∠C和ΔABC的面积.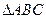 中,
中,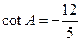 ,则
,则