题目内容
设函数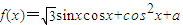 .
.(Ⅰ)写出函数的最小正周期及单调递减区间;
(Ⅱ)当x∈[
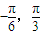 ]时,函数f(x)的最大值与最小值的和为
]时,函数f(x)的最大值与最小值的和为 ,求f(x)的解析式;
,求f(x)的解析式;(Ⅲ)将满足(Ⅱ)的函数f(x)的图象向右平移
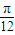 个单位,纵坐标不变横坐标变为原来的2倍,再向下平移
个单位,纵坐标不变横坐标变为原来的2倍,再向下平移 ,得到函数g(x),求g(x)图象与x轴的正半轴、直线
,得到函数g(x),求g(x)图象与x轴的正半轴、直线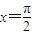 所围成图形的面积.
所围成图形的面积.
【答案】分析:(I)利用和差角公式,可将函数的解析式化为正弦型函数的形式,根据ω可得函数的周期,将相位角代入正弦函数的单调递减区间,求出x的范围,可得函数f(x)的单调递减区间
(II)由x的范围,可求出相位角的范围,进而根据正弦函数的图象和性质,可求出函数的最值,进而得到a值,求出函数的解析式
(III)根据函数图象的平移变换法则,伸缩变换法则,求出g(x)的解析式,代入积分公式,可得g(x)图象与x轴的正半轴、直线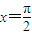 所围成图形的面积.
所围成图形的面积.
解答:解(Ⅰ)函数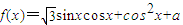 =
=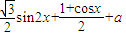 =sin(2x+
=sin(2x+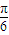 )+a+
)+a+ .
.
∵ω=2,
∴T=π
由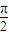 +2kπ≤2x+
+2kπ≤2x+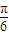 ≤
≤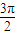 +2kπ,得
+2kπ,得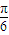 +kπ≤x≤
+kπ≤x≤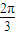 +kπ,(k∈Z),
+kπ,(k∈Z),
故函数f(x)的单调递减区间是[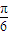 +kπ,
+kπ,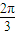 +kπ],(k∈Z).
+kπ],(k∈Z).
(II)∵x∈[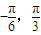 ]
]
∴2x+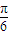 ∈[
∈[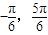 ]
]
∴sin(2x+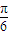 )∈[
)∈[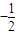 ,1]
,1]
∴当x∈[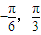 ]时,原函数的最大值与最小值的和
]时,原函数的最大值与最小值的和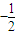 +a+
+a+ +1+a+
+1+a+ =
= ,
,
解得:a=0
∴f(x)=sin(2x+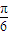 )+
)+
(3)将满足(Ⅱ)的函数f(x)sin(2x+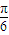 )+
)+ 的图象向右平移
的图象向右平移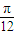 个单位,纵坐标不变横坐标变为原来的2倍,再向下平移
个单位,纵坐标不变横坐标变为原来的2倍,再向下平移 ,得到函数g(x)=sinx的图象
,得到函数g(x)=sinx的图象
∵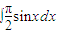 =-cosx
=-cosx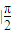 =1,即g(x)图象与x轴的正半轴、直线
=1,即g(x)图象与x轴的正半轴、直线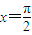 所围成图形的面积为1
所围成图形的面积为1
点评:本题考查的知识点是三角函数的化简,三角函数的周期性,单调性,最值,及函数图象的变换,是三角函数问题的综合应用,难度中档.
(II)由x的范围,可求出相位角的范围,进而根据正弦函数的图象和性质,可求出函数的最值,进而得到a值,求出函数的解析式
(III)根据函数图象的平移变换法则,伸缩变换法则,求出g(x)的解析式,代入积分公式,可得g(x)图象与x轴的正半轴、直线
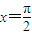 所围成图形的面积.
所围成图形的面积.解答:解(Ⅰ)函数
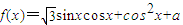 =
=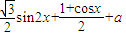 =sin(2x+
=sin(2x+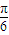 )+a+
)+a+ .
.∵ω=2,
∴T=π
由
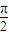 +2kπ≤2x+
+2kπ≤2x+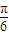 ≤
≤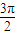 +2kπ,得
+2kπ,得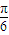 +kπ≤x≤
+kπ≤x≤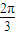 +kπ,(k∈Z),
+kπ,(k∈Z),故函数f(x)的单调递减区间是[
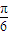 +kπ,
+kπ,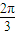 +kπ],(k∈Z).
+kπ],(k∈Z).(II)∵x∈[
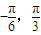 ]
]∴2x+
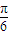 ∈[
∈[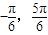 ]
]∴sin(2x+
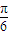 )∈[
)∈[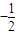 ,1]
,1]∴当x∈[
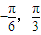 ]时,原函数的最大值与最小值的和
]时,原函数的最大值与最小值的和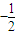 +a+
+a+ +1+a+
+1+a+ =
= ,
,解得:a=0
∴f(x)=sin(2x+
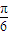 )+
)+
(3)将满足(Ⅱ)的函数f(x)sin(2x+
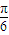 )+
)+ 的图象向右平移
的图象向右平移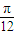 个单位,纵坐标不变横坐标变为原来的2倍,再向下平移
个单位,纵坐标不变横坐标变为原来的2倍,再向下平移 ,得到函数g(x)=sinx的图象
,得到函数g(x)=sinx的图象∵
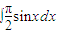 =-cosx
=-cosx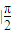 =1,即g(x)图象与x轴的正半轴、直线
=1,即g(x)图象与x轴的正半轴、直线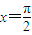 所围成图形的面积为1
所围成图形的面积为1点评:本题考查的知识点是三角函数的化简,三角函数的周期性,单调性,最值,及函数图象的变换,是三角函数问题的综合应用,难度中档.

练习册系列答案
相关题目
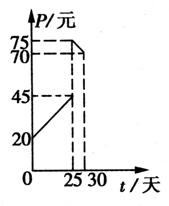
某种商品在30天内每件的销售价格P(元)与时间t(天) 的函数
关系用如图所示的两条直线段表示:
 又该商品在30天内日销售量Q(件)与时间t(天)之间的关系
又该商品在30天内日销售量Q(件)与时间t(天)之间的关系
如下表所示:
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 |
|
(1)根据题设条件,写出该商品每件的销售价格P与时间t的函
数关系式;并确定日销售量Q与时间t的一个函数关系式;
(2),试问30天中第几天日销售金额最大?最大金额为多少元?
(日销售金额=每件的销售价格×日销售量).
 ,写出
,写出