题目内容
【题目】已知函数
的图象关于直线
对称，则正确的选项是（ ）
①.函数
为奇函数
②.函数
在
上单调递增
③.若
，则
的最小值为
④.函数的图象向右平移
个单位长度得到函数
的图象
A.①③B.①④C.①②③D.②③④
【答案】A
【解析】
根据
关于直线
对称及
，解得
，所以
，对于①：
，即可判断①正误；对于②：
，所以
，即可判断②正误；对于③：因为
，
，结合题意
，以及的周期，可得
的最小值为半个周期，即可判断③正误；对于④，可得平移后的
，即可判断④正误.
由题意关于对称，所以
，
又，所以，所以
对于①：，为奇函数，故①正确；
对于②：，所以，所以函数在
上不单调，故②错误；
对于③：因为，，结合题意，所以的最小值为半个周期，又，
，所以的最小值为
，故③正确；
对于④：
的图像向右平移
个单位长度得到函数
，故④错误.
故选：A.
【题目】某校
位同学的数学与英语成绩如下表所示：
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
将这位同学的两科成绩绘制成散点图如下：
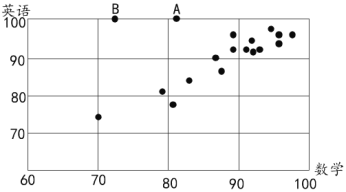
（1）根据该校以往的经验，数学成绩
与英语成绩
线性相关.已知这名学生的数学平均成绩为
，英语平均成绩为
.考试结束后学校经过调查发现学号为
的
同学与学号为
的
同学（分别对应散点图中的、）在英语考试中作弊，故将两位同学的两科成绩取消，取消两位作弊同学的两科成绩后，求其余同学的数学成绩与英语成绩的平均数；
（2）取消两位作弊同学的两科成绩后，求数学成绩与英语成绩的线性回归方程
，并据此估计本次英语考试学号为的同学如果没有作弊的英语成绩（结果保留整数）.
附：位同学的两科成绩的参考数据：
，
.
参考公式：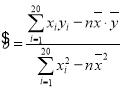
，
.
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查，每位市民仅有一次参加机会，通过随机抽样，得到参与问卷调查的100人的得分（满分：100分）数据，统计结果如表所示：
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”，请完成答题卡中的
列联表，并判断能否在犯错误概率不超过0.05的前提下，认为是否为“环保关注者”与性别有关？
(2)若问卷得分不低于80分的人称为“环保达人”．视频率为概率．
①在我市所有“环保达人”中，随机抽取3人，求抽取的3人中，既有男“环保达人”又有女“环保达人”的概率；
②为了鼓励市民关注环保，针对此次的调查制定了如下奖励方案：“环保达人”获得两次抽奖活动；其他参与的市民获得一次抽奖活动．每次抽奖获得红包的金额和对应的概率.如下表：
红包金额（单位：元） | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查，记
（单位：元）为该市民参加间卷调查获得的红包金额，求的分布列及数学期望．
附表及公式：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
