题目内容
已知定义在实数集R上的函数y=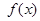 满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证:
满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证: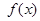 是奇函数;(3) 若
是奇函数;(3) 若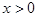 时,
时,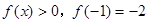 ,求
,求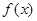 在
在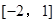 上的值域.
上的值域.
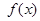 满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证:
满足条件:对于任意实数x、y都有f(x+y)=f(x)+f(y).(1)求f(0);(2) 求证: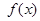 是奇函数;(3) 若
是奇函数;(3) 若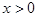 时,
时,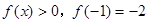 ,求
,求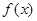 在
在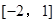 上的值域.
上的值域.(1)f(0)=0;(2)证明见解析;(3)证明见解析;值域[-4,2]。
本题考点是抽象函数及其运用,考查灵活赋值求函数值以及运用恒等式灵活变形证明函数的单调性,利用复合函数的单调性判断方程的根的个数,本题涉及到的考点较多,知识性与技巧性都很强,是知识完善结合的一个好题.
(1)令令x=y=0,代入恒等式f(x+y)=f(x)+f(y)即可求得.
(2)通过赋值法可知函数的奇偶性
(3)根据定义法证明函数的单调性然后,利用单调性得到值域。
(1)f(0)=0;3分
(2)证明略;9分
(3)证明单调性 13分
值域[-4,2] 15分
(1)令令x=y=0,代入恒等式f(x+y)=f(x)+f(y)即可求得.
(2)通过赋值法可知函数的奇偶性
(3)根据定义法证明函数的单调性然后,利用单调性得到值域。
(1)f(0)=0;3分
(2)证明略;9分
(3)证明单调性 13分
值域[-4,2] 15分

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
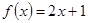 ,它的值域为
,它的值域为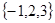 ,则该函数的定义域为 .
,则该函数的定义域为 .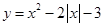 的递增区间为
的递增区间为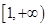 ;④定义在R上的函数
;④定义在R上的函数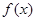 对任意两个不等实数a、b,总有
对任意两个不等实数a、b,总有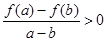 成立,则
成立,则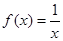 的单调减区间是
的单调减区间是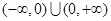 ;正确的有____________
;正确的有____________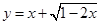 的值域是( )
的值域是( ) 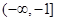
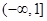
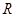

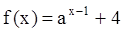 (
(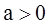 ,且
,且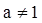 )恒过定点P,则点P的坐标为_________。
)恒过定点P,则点P的坐标为_________。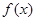 由下给出
由下给出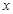
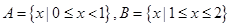 ,函数
,函数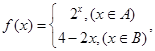
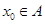 且
且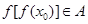 , 则
, 则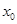 的取值范围是
的取值范围是 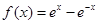 的定义域为
的定义域为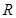 ,则 ( )
,则 ( ) 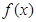 为奇函数,且为
为奇函数,且为