题目内容
在计算“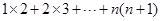 ”时,某同学学到了如下一种方法:先改写第k项:
”时,某同学学到了如下一种方法:先改写第k项: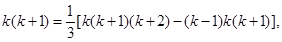 由此得
由此得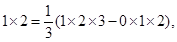
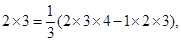
………… 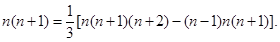
相加,得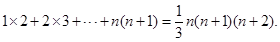
类比上述方法,请你计算“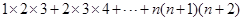 ”,
”,
其结果为 
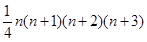
解析试题分析::∵n(n+1)(n+2)="1" 4 [n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]
∴1×2×3= (1×2×3×4-0×1×2×3)
(1×2×3×4-0×1×2×3)
2×3×4= (2×3×4×5-1×2×3×4)
(2×3×4×5-1×2×3×4)
…
n(n+1)(n+2)= [n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]
[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]
∴1×2×3+2×3×4+…+n(n+1)(n+2)= [(1×2×3×4-0×1×2×3)+(2×3×4×5-1×2×3×4)+…+n×(n+1)×(n+2)×(n+3)]-(n-1)×n×(n+1)×(n+2)=
[(1×2×3×4-0×1×2×3)+(2×3×4×5-1×2×3×4)+…+n×(n+1)×(n+2)×(n+3)]-(n-1)×n×(n+1)×(n+2)= n(n+1)(n+2)(n+3)
n(n+1)(n+2)(n+3)
故答案为: n(n+1)(n+2)(n+3)
n(n+1)(n+2)(n+3)
考点:进行简单的合情推理
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
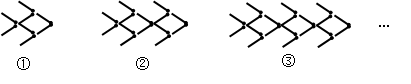
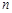 个“金鱼”图需要火柴棒的根数为 .
个“金鱼”图需要火柴棒的根数为 .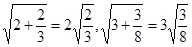 ,
,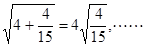 ,若
,若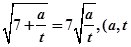 均为正实数),根据以上等式,可推测a,t的值,则
均为正实数),根据以上等式,可推测a,t的值,则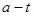 =_________.
=_________.
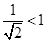 ;②
;②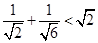 ;③
;③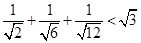 ;…
;…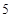 个不等式为 .
个不等式为 .
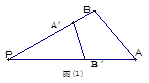
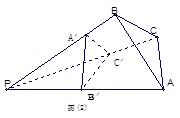
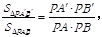 则由(2) 有体积关系:
则由(2) 有体积关系: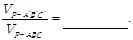
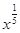 >
>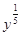 ”时,假设的内容应该是 .
”时,假设的内容应该是 . r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1、S2、S3、S4,则此四面体的体积V=________.