题目内容
7.求下列函数的值域:(1)y=$\frac{3x-1}{x+1}$(x≥5);
(2)y=x-$\sqrt{1-2x}$.
分析 (1)变形可得y=3-$\frac{4}{x+1}$,由x≥5结合不等式的性质可得;
(2)由1-2x≥0可得x≤$\frac{1}{2}$,结合函数单调递增可得.
解答 解:(1)变形可得y=$\frac{3x-1}{x+1}$=$\frac{3(x+1)-4}{x+1}$=3-$\frac{4}{x+1}$,
∵x≥5,∴x+1≥6,∴0<$\frac{4}{x+1}$≤$\frac{2}{3}$,
∴-$\frac{2}{3}$≤-$\frac{4}{x+1}$<0,
∴$\frac{7}{3}$≤3-$\frac{4}{x+1}$<3,
∴函数的值域为[$\frac{7}{3}$,3);
(2)由1-2x≥0可得x≤$\frac{1}{2}$,
又由复合函数单调性可得y=x-$\sqrt{1-2x}$单调递增,
∴当x=$\frac{1}{2}$时,函数取最大值$\frac{1}{2}$,
∴函数的值域为(-∞,$\frac{1}{2}$]
点评 本题考查函数的值域,涉及分类常数法和复合函数的单调性,属中档题.

练习册系列答案
相关题目
19.函数f(x)=ax2-2014x+2015(a>0),在区间[t-1,t+1](t∈R)上函数f(x)的最大值为M,最小值为N,当t取任意实数时.M-N的最小值为1,则a=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.设M={x|0≤x≤2},N={y|0≤y≤2},给出如图所示的四个图形:
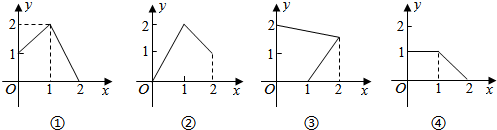
其中能表示从集合M到集合N的函数关系式的有( )

其中能表示从集合M到集合N的函数关系式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |