题目内容
（2012•衡阳模拟）命题p：m＞7，命题q：f （x）=x2+mx+9（m∈R）有零点，则p是q的（ ）
分析：已知命题q：f （x）=x2+mx+9（m∈R）有零点，△≥0，求出m的范围，再必要条件和充分条件的定义进行判断；
解答：解：∵命题p：m＞7，
命题q：f （x）=x2+mx+9（m∈R）有零点，△≥0，
△=m2-4×9≥0，∴m≥6或m≤-6，
∴命题p：m＞7⇒命题q：m≥6或m≤-6，反之则不能，
∴p是q充分不必要条件，
故选A．
命题q：f （x）=x2+mx+9（m∈R）有零点，△≥0，
△=m2-4×9≥0，∴m≥6或m≤-6，
∴命题p：m＞7⇒命题q：m≥6或m≤-6，反之则不能，
∴p是q充分不必要条件，
故选A．
点评：本题主要考查函数的零点及必要条件和充分条件的定义及其判断，是一道基础题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
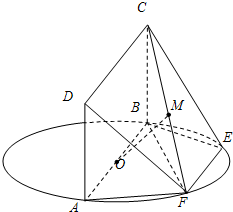（2012•衡阳模拟）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD的边BC垂直于圆O所在的平面，且AB=2，AD=EF=1．