题目内容
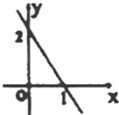已知函数y=f（x）的定义域为R，且满足f（1）=2，其导函数为f′（x）的图象如图，则函数y=f（x）的图象是（ ）分析：由导数与函数单调性的关系即可判断函数f（x）的大体图象．
解答：解：由f'（x）的图象知，当x＜1时，f'（x）＞0，当x＞1时，f'（x）＜0，
所以当x＜1时，f（x）单调递增，当x＞1时，f（x）单调递减．
故选C．
所以当x＜1时，f（x）单调递增，当x＞1时，f（x）单调递减．
故选C．
点评：本题主要考查了函数的图象以及导数与函数单调性的关系，本题只需根据函数单调性即可判断函数的图象．
练习册系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，当x＞0 时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]≤0 的解集为
已知函数y=f（x）的图象如图，则满足