题目内容
曲线
 在x=2处切线方程的斜率是( )
在x=2处切线方程的斜率是( )
A. 4 B. 2 C. 1 D. 
A
【解析】
试题分析:【解析】
因为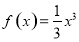 ,所以,
,所以,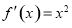
所以,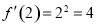 .故应选A.
.故应选A.
考点:导数的几何意义.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
题目内容
曲线
 在x=2处切线方程的斜率是( )
在x=2处切线方程的斜率是( )
A. 4 B. 2 C. 1 D. 
A
【解析】
试题分析:【解析】
因为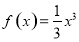 ,所以,
,所以,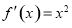
所以,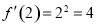 .故应选A.
.故应选A.
考点:导数的几何意义.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案