题目内容
10.袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求点(x,y)满足(x-1)2+y2≤9的概率.
分析 (1)(2)分别列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算,问题得以解决.
解答 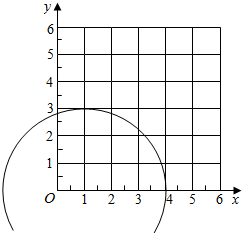 解:(1)任取2次,基本事件有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10个,
解:(1)任取2次,基本事件有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10个,
其中两个小球所标数字之和为3的倍数的基本事件有(1,2),(1,5),(2,4),(4,5)共4个,
故两个小球所标数字之和为3的倍数的概率P=$\frac{4}{10}$=$\frac{2}{5}$;
(2)有放回的取2个,基本事件有5×5=25个,满足点(x,y)满足(x-1)2+y2≤9的有如图所示),(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),(3,2)共7个,
故点(x,y)满足(x-1)2+y2≤9的概率P=$\frac{7}{25}$
点评 本题考查古典概型的概率问题,关键是不重不漏的列举基本事件,第二问,采取数形结合比较好列举,属于基础题.

练习册系列答案
相关题目
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-y-3≤0}\\{x-2y≥0}\\{x+y-3≥0}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
18.已知正方体的棱长为2$\sqrt{3}$,则外接球的体积为( )
| A. | 36π | B. | 288π | C. | 12π | D. | 18π |
2.复数z=-4i+3的虚部是( )
| A. | -4i | B. | 3i | C. | 3 | D. | -4 |
19.已知函数f(x)=sinx,f(x)的导数是( )
| A. | 偶函数 | B. | 奇函数 | C. | 增函数 | D. | 减函数 |
20.样本中共有五个个体,其值分别为-1,0,2,3,a,若该样本的平均值为1,则样本方差为( )
| A. | $\sqrt{\frac{6}{5}}$ | B. | $\frac{6}{5}$ | C. | $\sqrt{2}$ | D. | 2 |